Количественная теория полезности
| Аддитивная функция полезности |
Экономисты XIX века (Уильям Джевонс, Леон Вальрас), как основоположники кардиналистского (количественного) подхода к оценке полезности потребителя, предполагали, что потребитель способен оценить потребляемые им товары с точки зрения величины полезности, причем целью потребителя является максимизация полезности. Поэтому первоначально полезность набора благ представлялась как сумма полезностей всех входящих в комплект благ, то есть использовалась аддитивная функция полезности:
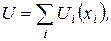 (4.10)
(4.10)
где 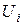 – полезность блага
– полезность блага 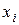 .
.
Следовательно, предполагалась независимость полезностей отдельных благ друг от друга.
В современной теории многокритериального выбора решений вид (4.10) агрегированного критерия по-прежнему широко распространен, однако вводится зависимость альтернатив по полезности, выражаемая коэффициентами значимости 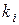 :
:
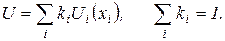 (4.11)
(4.11)
Функции полезности, рассмотренные выше, также являются аддитивными функциями вида (4.11).
Пример 4.3.1. Провести упорядочение по полезности альтернативных проектов трех моделей автомобилей при следующих значениях критериев (объемов благ) и коэффициентов значимости:
| № п/п | Критерий (благо) | Модель | Коэффициент значимости | ||
| 1-я | 2-я | 3-я | |||
| 1 | Цена, тыс. руб | 28 | 30 | 30 | 0,4 |
| 2 | Полезный объем, м3 | 4 | 5 | 6 | 0,1 |
| 3 | Расходы на обслуживание, тыс. руб. | 3 | 1 | 2 | 0,2 |
| 4 | Скорость, км/ч | 180 | 180 | 200 | 0,3 |
Определим полезность блага 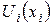 как возрастающую безразмерную функцию объема блага
как возрастающую безразмерную функцию объема блага 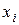 , то есть большему количеству блага должно соответствовать большее значение его полезности:
, то есть большему количеству блага должно соответствовать большее значение его полезности:
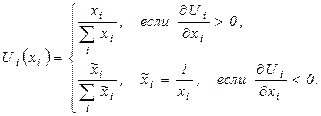
Расчет частных полезностей проведен в таблице:
| Номер критерия | 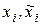
| 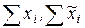
| 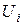
| ||||
| Модель | Модель | ||||||
| 1-я | 2-я | 3-я | 1-я | 2-я | 3-я | ||
| 1 | 1/28 | 1/30 | 1/30 | 0,1024 | 0,35 | 0,33 | 0,33 |
| 2 | 4 | 5 | 6 | 15 | 0,27 | 0,33 | 0,40 |
| 3 | 1/3 | 1 | 1/2 | 1,833 | 0,18 | 0,55 | 0,27 |
| 4 | 180 | 180 | 20 | 560 | 0,32 | 0,32 | 0,36 |
Полезности моделей с учетом коэффициентов значимости равны:
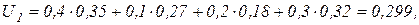
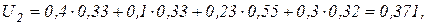
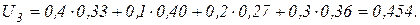
Итак, модели предпочтительны в следующем порядке:
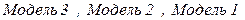
| Законы Госсена |
Цель максимизации количественной полезности нашла выражение в закономерностях, полученных немецким экономистом Германом Госсеном в 1854 г. в работе «Развитие законов общественного обмена и вытекающих отсюда правил человеческой деятельности».
Первый закон Госсена: в одном непрерывном акте потребления полезность последующей единицы блага убывает; при повторном акте потребления полезность каждой единицы блага уменьшается по сравнению с ее полезностью при первоначальном потреблении.
Математическая запись этого закона имеет вид:
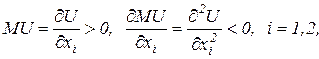 (4.12)
(4.12)
то есть предельная полезность блага по мере его потребления уменьшается.
Этот закон также получил название «аксиомы ненасыщения», поскольку при 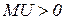 функция полезности возрастающая, то есть насыщение потребителя не наступает. Рассмотренные виды функции полезности удовлетворяют аксиоме ненасыщения.
функция полезности возрастающая, то есть насыщение потребителя не наступает. Рассмотренные виды функции полезности удовлетворяют аксиоме ненасыщения.
Первый закон Госсена был получен эмпирическим путем на основе обобщения субъективных мнений о полезности потребления благ в различных количествах.
Пример 4.3.2. Потребитель, рассмотренный в примере 4.2.1, приобретал 10 литров молока и 2 тюбика зубной пасты в месяц, и при логарифмической функцией полезности 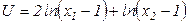 его удовлетворение от дополнительного литра молока составляло
его удовлетворение от дополнительного литра молока составляло 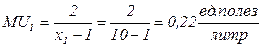 . Если же данный потребитель будет приобретать 30 литров молока в месяц, то увеличение закупок молока на 1 литр принесет ему дополнительно
. Если же данный потребитель будет приобретать 30 литров молока в месяц, то увеличение закупок молока на 1 литр принесет ему дополнительно 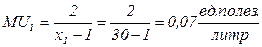 , то есть предельная полезность уменьшится.
, то есть предельная полезность уменьшится.
Второй закон Госсена: максимум полезности потребляемых благ за ограниченный период времени достигается, если затраты времени на потребление каждого блага таковы, что предельные полезности благ одинаковы.
Речь идет о задаче определения условного экстремума функции полезности
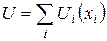
при ограниченном времени потребления благ
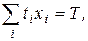
где 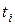 - время потребления единицы i-го блага,
- время потребления единицы i-го блага, 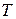 - располагаемый фонд времени. Задача решается методом множителей Лагранжа; функция Лагранжа имеет вид:
- располагаемый фонд времени. Задача решается методом множителей Лагранжа; функция Лагранжа имеет вид:
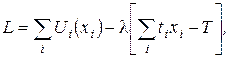 (4.13)
(4.13)
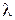 - множитель Лагранжа.
- множитель Лагранжа.
Необходимые условия оптимальности определяются системой уравнений:
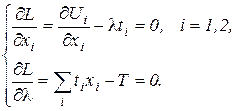
Из первого уравнения системы следует:
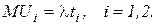 (4.14)
(4.14)
Деление одного уравнения (4.14) на другое приводит к соотношению:
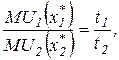 (4.15)
(4.15)
то есть наклон линии ограниченного времени (линия Т на рис. 4.6) должен быть равен наклону касательной к кривой безразличия U при оптимальных объемах потребления благ.
 |
Рис. 4.6. Второй закон Госсена
Введем координаты 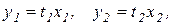 выражающие интервалы времени, затрачиваемые на потребление благ. Кривая безразличия будет представлена в новых координатах функцией полезности:
выражающие интервалы времени, затрачиваемые на потребление благ. Кривая безразличия будет представлена в новых координатах функцией полезности:
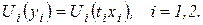
Предельные полезности благ равны:
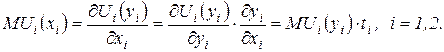
Подставив это условие в соотношение (6), можно получить:
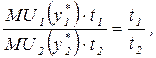
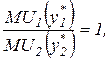
то есть в момент окончания потребления каждого блага предельные полезности всех благ одинаковы.
Экономический смысл множителя Лагранжа 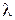 состоит в том, что прирост фонда времени Т на единицу приведет к увеличению полезности набора на
состоит в том, что прирост фонда времени Т на единицу приведет к увеличению полезности набора на 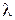 (из уравнения (4.13)), то есть
(из уравнения (4.13)), то есть
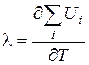
представляет собой предельную полезность времени.
Пример 4.3.3. Самолет летчика А. Ляпидевского, доставивший продукты героям-челюскинцам, зимовавшим на льдине в Северном ледовитом океане, имел возможность продолжать стоянку в течение 2 часов. Определить, какое количество хлеба (1-й товар) и одежды (2-й товар) полярники должны разгрузить, чтобы их полезность была максимальна, если их предпочтения выражает степенная функция вида 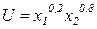 . Сколько времени они должны затратить на разгрузку каждого товара, если 1 кг хлеба можно разгрузить за 3 мин., а упаковку одежды за 5 минут.
. Сколько времени они должны затратить на разгрузку каждого товара, если 1 кг хлеба можно разгрузить за 3 мин., а упаковку одежды за 5 минут.
Выражения предельных полезностей имеют вид:
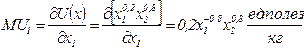 ,
, 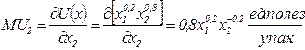 .
.
Приравняв эти выражения, получим 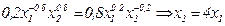 . Учитывая затраты времени на разгрузку, составим уравнение фонда времени:
. Учитывая затраты времени на разгрузку, составим уравнение фонда времени: 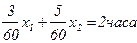 . Откуда находим количества товаров, которые необходимо разгрузить, чтобы максимизировать полезность зимовщиков:
. Откуда находим количества товаров, которые необходимо разгрузить, чтобы максимизировать полезность зимовщиков: 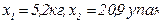 . Поэтому на разгрузку хлеба они должны потратить
. Поэтому на разгрузку хлеба они должны потратить 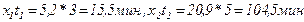 .
.
| Закон спроса |
Основным результатом количественной теории полезности стал закон спроса, полученный американским экономистом Альфредом Маршаллом в 1927 г. в работе "Принципы экономики". Маршалл исходил из того, что предельная полезность денег[3], равная отношению предельной полезности блага к его цене, остается постоянной:
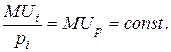
Это объясняется тем, что, по второму закону Госсена, потребитель максимизирует свою полезность путем потребления широкого ассортимента товаров, следовательно, изменение цены одного товара не повлияет на покупательную способность денег в целом. Отсюда следует, что предельная полезность блага пропорциональна его цене:
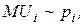
а поскольку, согласно первому закону Госсена, предельная полезность обратно пропорциональна объему потребления блага 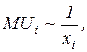 то
то 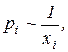 то есть кривая спроса является убывающей. В этом состоит закон спроса.
то есть кривая спроса является убывающей. В этом состоит закон спроса.
Дата добавления: 2020-10-25; просмотров: 674;











