Виды функции полезности
| Логарифмическая функция |
В работе «Опыт новой теории измерения жребия», опубликованной в 1738 г., швейцарский математик Даниил Бернулли впервые предложил способ количественного определения полезности блага на основе вероятностной теории игр. Полезность (или выгода) U есть результат, получаемый потребителем от обладания благом (достижения выигрыша) x. Диапазон изменения объема потребления блага x разбивается на два интервала:
1) при 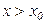 благо обеспечивает доход (полезность); значение
благо обеспечивает доход (полезность); значение 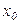 есть объем блага, соответствующий нулевому уровню полезности;
есть объем блага, соответствующий нулевому уровню полезности;
2) при 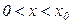 располагаемый объем блага снижает уровень удовлетворенности (приводит к убытку); причем чем меньше имеющийся объем блага, тем существеннее снижение удовлетворенности потребителя; иначе говоря, это интервал «антиблага».
располагаемый объем блага снижает уровень удовлетворенности (приводит к убытку); причем чем меньше имеющийся объем блага, тем существеннее снижение удовлетворенности потребителя; иначе говоря, это интервал «антиблага».
 |
Рис. 4.3. Вид кривой полезности
 С точки зрения теории игр благо интерпретируется как выигрыш, а «антиблаго» – как сумма ставки, необходимая для получения соответствующего выигрыша (рис. 4.3). В игре со справедливыми условиями убыток от проигрыша должен быть равен выгоде от выигрыша, то есть при
С точки зрения теории игр благо интерпретируется как выигрыш, а «антиблаго» – как сумма ставки, необходимая для получения соответствующего выигрыша (рис. 4.3). В игре со справедливыми условиями убыток от проигрыша должен быть равен выгоде от выигрыша, то есть при
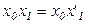
должно выполняться условие
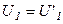 .
.
Рис. 4.4. Предположение Бернулли
В дальнейших рассуждениях Д. Бернулли использовал следующее предположение: объем блага 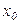 , соответствующий полной неудовлетворенности потребителя (U=0), несопоставим с максимально возможным объемом потребления блага
, соответствующий полной неудовлетворенности потребителя (U=0), несопоставим с максимально возможным объемом потребления блага 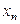 , то есть
, то есть 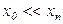 .
.
В этом случае дугу 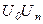 можно рассматривать как кривую, близкую к отрезку прямой линии, угловой коэффициент которой, как видно из рис. 4.4, равен
можно рассматривать как кривую, близкую к отрезку прямой линии, угловой коэффициент которой, как видно из рис. 4.4, равен 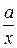 ; параметр а представляет собой длину подкасательной (проекции значения функции на ось аргумента), если рассматривать зависимость х от U.
; параметр а представляет собой длину подкасательной (проекции значения функции на ось аргумента), если рассматривать зависимость х от U.
Для получения уравнения кривой 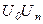 значению имеющегося блага
значению имеющегося блага 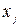 дается бесконечно малое приращение dx, приводящее к соответствующему приросту полезности dU. С учетом принятого предположения угловые коэффициенты дуги
дается бесконечно малое приращение dx, приводящее к соответствующему приросту полезности dU. С учетом принятого предположения угловые коэффициенты дуги 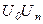 и дуги
и дуги 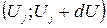 как отрезка кривой, равны:
как отрезка кривой, равны:
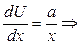 ,
, 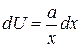 . (4.5)
. (4.5)
Решением дифференциального уравнения (4.5) является функция:
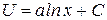
с начальным условием 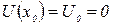 , откуда
, откуда
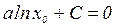 ,
, 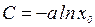 ,
,
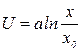 . (4.6)
. (4.6)
Таким образом, функция полезности представляет собой логарифмическую кривую, подкасательная которой равна а, асимптота – ось ординат. Поэтому сумма дохода и убытка (длина подкасательной а)остается постоянной для любых игровых ситуаций, так как рассматривается игра с полной суммой.
Однако функция полезности вида (4.6), имеющая адекватную игровую интерпретацию, не нашла широкого применения в теории полезности, так как на интервале 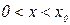 функция (4.6) принимает отрицательные значения.
функция (4.6) принимает отрицательные значения.
Более распространена логарифмическая функция Бернулли, полученная путем смещения дуги 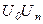 параллельно самой себе влево до совпадения точки
параллельно самой себе влево до совпадения точки 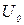 с точкой, абсцисса которой х=1, то есть при сдвиге на величину
с точкой, абсцисса которой х=1, то есть при сдвиге на величину 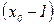 :
:
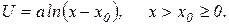
Для случая нескольких благ логарифмическая функция записывается в виде:
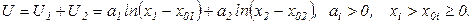 (4.7)
(4.7)
Экономический смысл коэффициентов логарифмической функции: 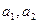 – характеризуют вклад товаров в совокупную полезность потребителя;
– характеризуют вклад товаров в совокупную полезность потребителя; 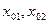 - показывают количества товаров, при которых потребитель ощущает неудовлетворенность, выражают т.н. «уровни бедности».
- показывают количества товаров, при которых потребитель ощущает неудовлетворенность, выражают т.н. «уровни бедности».
Логарифмическая функция полезности применяется для описания предпочтений потребителя, который может быть удовлетворен при отсутствии полезного вклада какого-либо блага, то есть если блага являются субститутами.
Пример 4.2.1. Предпочтения потребителя, приобретающего 10 литров молока и 2 тюбика зубной пасты в месяц, выражаются логарифмической функцией полезности с коэффициентами 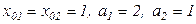 . Потребитель рассуждает о том, что ему полезнее: приобрести дополнительно 1 литр молока или 1 тюбик пасты?
. Потребитель рассуждает о том, что ему полезнее: приобрести дополнительно 1 литр молока или 1 тюбик пасты?
Запишем функцию полезности потребителя: 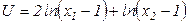 . Для ответа на вопрос потребителю нужно сравнить предельные полезности молока и пасты при данном объеме потребления этих товаров. Вычислим предельные полезности по формуле (4.1):
. Для ответа на вопрос потребителю нужно сравнить предельные полезности молока и пасты при данном объеме потребления этих товаров. Вычислим предельные полезности по формуле (4.1):
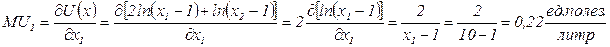 ,
,
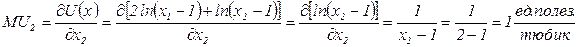 .
.
Таким образом, потребителю значительно полезнее приобрести дополнительно тюбик пасты, чем литр молока.
| Степенная функция |
Продолжая игровую интерпретацию (рис. 4.3), Д. Бернулли ввел понятие среднего выигрыша (среднего значения полезности):
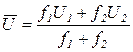
где 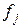 - частота получения j-го блага (наступления j-го выигрыша).
- частота получения j-го блага (наступления j-го выигрыша).
Полагая а1=а2=а, то есть считая сумму дохода и убытка одинаковой для всех рассматриваемых товаров, получим формулу средней полезности:
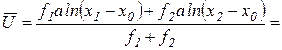
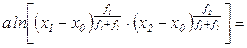
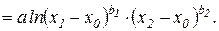
Поскольку логарифмическая функция является возрастающей, то подлогарифмическое выражение также представляет собой функцию полезности:
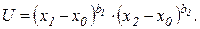
В общем виде степенная функция записывается следующим образом:
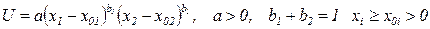 (4.8)
(4.8)
Экономический смысл коэффициентов степенной функции: 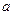 – коэффициент перевода единиц измерения товаров в измерители полезности потребителя, например, при необходимости измерения полезности в денежной форме;
– коэффициент перевода единиц измерения товаров в измерители полезности потребителя, например, при необходимости измерения полезности в денежной форме; 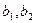 – характеризуют относительный (в процентах) вклад товаров в совокупную полезность потребителя.
– характеризуют относительный (в процентах) вклад товаров в совокупную полезность потребителя.
Функция (4.8) применяется для описания предпочтений потребителя, который не удовлетворен при отсутствии полезного вклада хотя бы одного блага.
Смысл теории игр, вложенный Д. Бернулли в функцию средней полезности, позволил интерпретировать полезность в задачах определения первоначального объема блага, необходимого для достижения определенного уровня полезности, и прироста удовлетворения, связанного с приращением располагаемого объема блага. В этом случае предполагается, что речь идет об одном благе, которое может иметься в различных количествах, и, следовательно, обеспечивать разный уровень удовлетворенности.
Пример 4.2.2. Продавец планирует реализовать товар за 10 000 руб., однако, как правило, из 100 сделок аналогичного типа 5 оказываются неудачными. Сделка может быть застрахована за 800 руб. Определить: а) начиная с какой суммы капитала продавец может отказаться от страховки; б) каким минимальным капиталом должен располагать страховщик, чтобы ему были выгодны такие условия страхования.
Определим размер начального капитала продавца 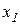 , считая
, считая 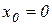 ,
, 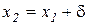 ,
, 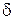 - прирост капитала. Приравняем среднюю полезность при отказе от страховки
- прирост капитала. Приравняем среднюю полезность при отказе от страховки 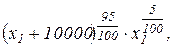 и при согласии застраховать сделку
и при согласии застраховать сделку 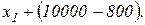 Уравнение
Уравнение
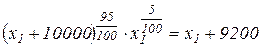
имеет приближенное решение 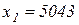 . Поэтому если капитал продавца превышает сумму 5043 руб., то прирост средней полезности в случае отказа от страховки выше, чем в случае ее принятия.
. Поэтому если капитал продавца превышает сумму 5043 руб., то прирост средней полезности в случае отказа от страховки выше, чем в случае ее принятия.
Размер начального капитала страховщика определим из условия равенства его средней полезности при принятии на себя страхования и при отказе от страхования:
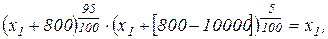
откуда 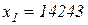 . Таким образом, если страховщик имеет капитал, превышающий 14243 руб., то ему полезнее взять на себя обязанности страхования, чем отказаться от них.
. Таким образом, если страховщик имеет капитал, превышающий 14243 руб., то ему полезнее взять на себя обязанности страхования, чем отказаться от них.
Пример 4.2.3. Предприниматель имеет товары на складе на сумму 4000 руб. и товары отгруженные на сумму 8000 руб., причем, как правило, десятая часть отгруженных товаров не оплачивается покупателями. Определить полезность запасов предпринимателя.
По формуле средней полезности:
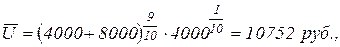
а за вычетом оставшихся на складе товаров полезность отгруженных товаров равна 6752 руб.
Рассмотренные примеры показывают, что полезность (степень удовлетворенности) может быть количественно оценена.
| Функция Аллена |
Английский экономист Рой Джордж Аллен (1906-1983) предложил вид функции полезности, которая получила название квадратической или функции Аллена.
Основной предпосылкой выбора вида функции было существование потребителей, для которых возможность пользования определенными благами ограничена, вследствие чего чрезмерный рост объема одного из благ при неизменном объеме потребления другого снижает общую полезность.
 Рис. 4.5. Функция Аллена
Рис. 4.5. Функция Аллена
Иначе говоря, полезность выражается абсолютной величиной отклонения объемов потребления благ друг от друга, взятой с обратным знаком:
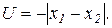
Более удобной является дифференцируемая функция полезности, поэтому функцию модуля целесообразно заменить на квадратическую функцию:
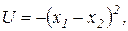
или в более общем виде:
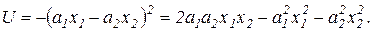 (4.9)
(4.9)
Функция Аллена, вид которой при фиксированном объеме потребления первого блага показан на рис. 4.5, всегда отрицательна и представляет собой «функцию потерь», которые несет потребитель если располагаемые объемы благ отличаются от заданных удельных потребностей 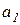 и
и 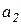 :
:
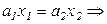
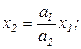
только в этом случае потери равны нулю и «полезность» максимальна.
Дата добавления: 2020-10-25; просмотров: 770;











