Кооперативная дуполия

Дуполисты могут вступить в соглашение о совместной деятельности на рынке с целью получения максимальной совокупной прибыли так называемого простого товарищества. В этом случае условия выбора оптимальных значений объемов выпуска дуполистов имеют вид:

.

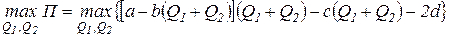Оптимальная программа выпуска фирм должна удовлетворять условию:

,

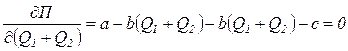так что

.

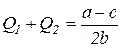Рыночная цена в условиях кооперации установится на уровне:

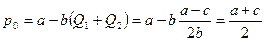
При равных производственных возможностях каждая фирма производит продукцию в объеме:

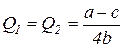. (3.31)

Сумму совокупной прибыли дуполистов определим, подставив объемы продукции (3.31) в формулу прибыли дуполии (3.23):

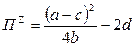. (3.32)

На рис. 3.11 показаны кривые реакции Курно для первой 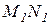и второй 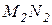фирм, берущие начало из монопольных точек фирм М₁ и М₂, то есть значений объемов выпуска этих фирм, полученных при условии, что вторая фирма отсутствует. Например, для первой фирмы:

,

.

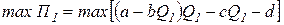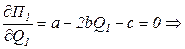
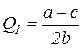Рис. 3.11. Типы дуполии

Точки 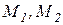также являются точками максимально возможной прибыли каждого дуполиста, то есть центрами семейств изопрофит (кривых равной прибыли): каждая изопрофита, расположенная на большем расстоянии от точки 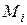, соответствует меньшей прибыли i-й фирмы. Точки касания изопрофиты одной фирмы и кривой реакции Курно другой фирмы являются точками равновесия Стэкельберга.

Неравновесие Стэкельберга (точка С на рис. 3.11) располагается выше и правее равновесия Курно (точка К на рис. 3.11), поскольку поведение обеих фирм в условиях неверных предположений о стратегии конкурентов (гипотеза Стэкельберга) близко к монополистическому образу действий.

Кооптимальная линия 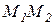имеет полученное выше уравнение

,

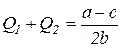и представляет собой множество точек касания изопрофит двух фирм.

Таким образом, в пределах кооптимальной линии ни одна из фирм не может увеличить свою прибыль, не уменьшив прибыль конкурента. Иначе говоря, сочетания объемов выпуска фирм на этой прямой являются равноэффективными точками для кооперативной дуполии, а сама линия определяет множество Парето для дуполистов, стремящихся наращивать индивидуальную прибыль.

Пример 3.11.1. Рассмотрим две организации–дуполиста, у которых постоянные издержки отсутствуют, а удельные переменные издержки равны 1010 рублей на единицу выпуска; функция издержек имеет вид:

.

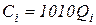Предположим, что максимальная цена, которую готов заплатить покупатель, составляет 1022 рубля, а при появлении на рынке каждой дополнительной единицы выпуска цена понижается на 0,5 рубля, то есть функция спроса:

.

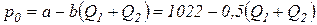В этом случае .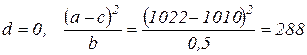

1) В условиях равновесия Курно суммы прибыли каждой из фирм по формуле (3.27) равны:

,

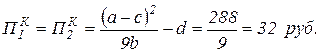значит совокупная прибыль дуполии Курно составит (32+32)=64 руб.

2) При равновесии Стэкельберга первая фирма получит прибыль (формула (3.28)) 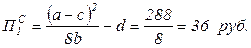, а вторая фирма (формула (3.29)): 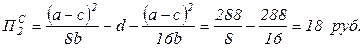Поэтому сумма прибыли дуполистов при этом равна (36+18)=54 руб.

3) В условиях неравновесия Стэкельберга суммы прибыли обеих фирм одинаковы (формула (3.30)):

,

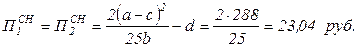то есть совокупная прибыль дуполии равна (2*23,04)=46,08 руб.

4) При кооперативной дуполии совокупная прибыль (формула (3.32)) составит 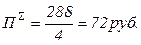, то есть наибольшая из всех рассмотренных вариантов.

Таким образом потери прибыли являются платой за конкурирующий характер стратегий дуполистов.