Анализ безубыточности
Методика планирования на основе исследованной в предыдущих параграфах задачи коммерческой организации нашла применение при анализе безубыточности производственной программы организации.
Безубыточность – это такое финансово-хозяйственное состояние, при котором доход фирмы равен издержкам. Объем производства, при котором достигается состояние безубыточности, называется критическим.
При этом делаются следующие предположения:
· рассматривается модель совершенной конкуренции, следовательно значение предельного дохода постоянно и равно цене продукта, следовательно линия дохода есть прямая;
· отдача от расширения масштаба производства предполагается постоянной; поэтому график функции издержек представляет собой прямую линию;
· рассматривается краткосрочный период планирования, вследствие чего функция издержек представляется в виде суммы постоянных и переменных издержек.
С учетом сделанных предположений используются следующие подходы к проблеме оценки рентабельности плана производства:
1. Сопоставление валового дохода R(Q) с валовыми издержками С(Q) и отделение зоны прибыли от зоны убытка (рис. 3.6). Выражение для критического объема производства получим из условия равенства доходов и расходов:
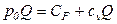 ,
,
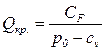 .
.
где 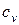 - удельные (средние) переменные издержки.
- удельные (средние) переменные издержки.
Значение объема выпуска 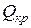 , при котором достигается безубыточность в условиях покрытия переменных и постоянных издержек ценой реализации, называется критическим значением.
, при котором достигается безубыточность в условиях покрытия переменных и постоянных издержек ценой реализации, называется критическим значением.
2. Сопоставление среднего дохода АR(Q)=р0 и средних издержек АС(Q), определяющее те же зоны прибыли и убытка (рис. 3.7).
3. Сопоставление предельного дохода МR(Q) и предельных издержек МС(Q), выявляющее возможность дальнейшей деятельности организации (рис. 3.7). Поскольку для модели совершенной конкуренции
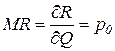 ,
,
а в условиях краткосрочного периода предельные издержки равны средним переменным издержкам
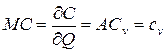 ,
,
то в этом случае необходимо сравнить значение цены продукта и величину удельных переменных издержек; так, на рис. 3.7 в случае 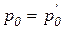 деятельность организации безубыточна при
деятельность организации безубыточна при
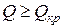 ,
,
а при
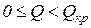
возможно дальнейшее функционирование организации, поскольку
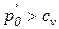 ;
;
однако в случае 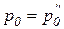 безубыточная работа невозможна и организация должна быть ликвидирована, так как
безубыточная работа невозможна и организация должна быть ликвидирована, так как
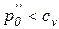 .
.
 |
Рис. 3.6. Анализ "валовой доход - валовые издержки"
Такой же вывод следует из рис. 3.6, так как сумма выручки при любом объеме выпуска меньше суммы переменных затрат в случае 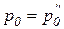 :
:
 ,
,
а при 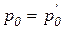 выполняется условие
выполняется условие
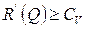 .
.
 |
Рис. 3.7. Анализ "предельный доход - предельные издержки"
Пример 3.5.1. Объем продукции мебельного комбината за месяц составляет 100 стульев, цена продукции 5 руб. Переменные издержки равны 2 руб. на единицу продукции, сумма косвенных (постоянных) расходов равна 110 руб. Оценить программу производства с точки зрения безубыточности.
Критический объем продукции определяется из условия равенства валового дохода и валовых издержек; он равен 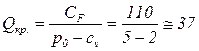 стульев. Поэтому текущая производственная программа безубыточна.
стульев. Поэтому текущая производственная программа безубыточна.
§3.6. Рациональная коммерческая деятельность в условиях
монополии и монопсонии
| Черты монополии и монопсонии |
Многие производители, специализирующиеся на выпуске слабо стандартизированных товаров или осваивающие уникальные, не имеющие аналогов, виды продукции, сталкиваются с условиями монополии (или монополистической конкуренции). Монополия ( 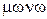 – один,
– один, 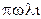 – продавать), в отличие от совершенной конкуренции, характеризуется зависимостью цены товара от объема рынка, то есть кривая спроса на монополизированный продукт имеет вид:
– продавать), в отличие от совершенной конкуренции, характеризуется зависимостью цены товара от объема рынка, то есть кривая спроса на монополизированный продукт имеет вид:
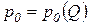 .
.
Следовательно, спрос на монополизированный продукт не является бесконечно эластичным; напротив, кривая спроса в этом случае убывающая.
Вместе с тем, в условиях монополии производитель обладает возможностью влиять на цену реализуемого товара путем варьирования объема предложения, учитывая, что
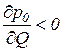 ,
,
то есть для увеличения объема продаж необходимо снижать цену и, наоборот, для увеличения цены необходимо уменьшить объем предложения.
Зачастую организация, занимающаяся производством специфического вида продукции, является преобладающим покупателем собственных поставщиков, которые, в свою очередь, вынуждены производить сырье, материалы, полуфабрикаты и комплектующие изделия в строгом соответствии с требованиями, предъявляемыми заказчиком. В этом случае продукция поставщиков также становится нестандартизированной и может быть реализована в пределах узкоспециализированного рынка. Ситуация, при которой существует тесная взаимосвязь между поставщиком и покупателем, является обратной стороной монополии и носит название монопсонии.
В условиях монопсонии ( 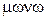 – один,
– один, 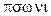 – покупать) покупатель имеет возможность оказывать влияние на цену приобретаемых у поставщиков ресурсов путем варьирования объема закупок, то есть существует зависимость вида:
– покупать) покупатель имеет возможность оказывать влияние на цену приобретаемых у поставщиков ресурсов путем варьирования объема закупок, то есть существует зависимость вида:
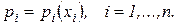
Эта функция характеризует сумму затрат покупателя – монопсониста на приобретение ресурсов 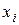 .
.
В общем случае покупатель может приобрести большее количество ресурса, предложив более высокую плату за него, то есть
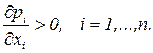
| Задача коммерческой организации |
Поскольку валовой доход организации определяется как
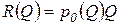 ,
,
а сумма издержек равна
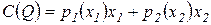 ,
,
то в условиях несовершенной конкуренции (комбинации монополии и монопсонии) задача рациональной коммерческой деятельности имеет вид:
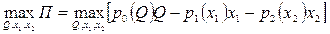
при условии
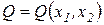 .
.
Предельный доход в этом случае, в отличие от совершенной конкуренции, не равен постоянной цене товара, которая определяется выражением 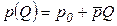 , а также зависит от объема выпуска:
, а также зависит от объема выпуска:
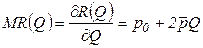 , (3.15)
, (3.15)
где производная 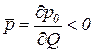 показывает, на сколько рублей снижается цена продукции от своего начального значения р0 при увеличении объема предложения фирмы на единицу.
показывает, на сколько рублей снижается цена продукции от своего начального значения р0 при увеличении объема предложения фирмы на единицу.
Предельные издержки в условиях монопсонии, если цена ресурса равна  , также зависят от объемов потребляемых ресурсов:
, также зависят от объемов потребляемых ресурсов:
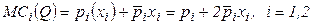 .
.
где 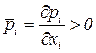 – рост цены ресурса при увеличении его закупок на единицу.
– рост цены ресурса при увеличении его закупок на единицу.
§3.7. Оптимальный план производства в условиях монополии и монопсонии
| Аналитическое решение |
Решение задачи коммерческой организации может быть получено методом множителей Лагранжа:
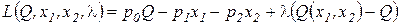 .
.
Необходимые условия экстремума определяются приравниванием нулю всех частных производных функции Лагранжа:
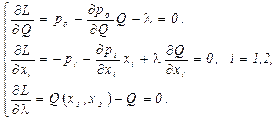
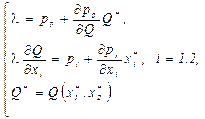
Первое условие показывает, что при оптимальных значениях 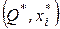 множитель Лагранжа равен предельному доходу:
множитель Лагранжа равен предельному доходу:
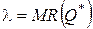 .
.
Вторая группа условий показывает, что произведение предельного дохода и предельного продукта каждого фактора равно предельным издержкам этого фактора:
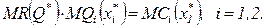 (3.16)
(3.16)
В последнем условии представлена просто производственная функция:
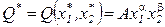 . (3.17)
. (3.17)
Условия (3.16),(3.17) являются исходными уравнениями определения объема выпуска и комбинации затрат ресурсов, максимизирующих прибыль. Кроме того, следует учитывать, что ранее полученное условие равенства предельного дохода предельным издержкам сохраняет силу и при монополии – монопсонии:
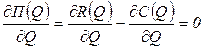 ,
,
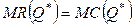 . (3.18)
. (3.18)
Используем выражение (3.18) для получения формулы оптимального объема производства в рамках монополии (ситуация монопсонии не учитывается, то есть предельные издержки зависят только от объема выпуска по формуле (2.9)). Рассмотрим два частных случая:
а) отрицательный эффект расширения масштаба при r=0,5; подставим в (3.18) выражение предельного дохода (3.15) и предельных издержек (2.9):
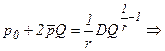
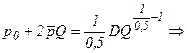
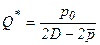 (3.19)
(3.19)
б) отсутствие эффекта расширения масштаба при r=1; аналогично предыдущему случаю:
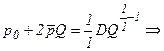
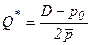 (3.20)
(3.20)
Функции спроса на ресурсы можно получить из условий (3.16), (3.17). выражения предельных продуктов MQi получены в примере 1.3.3:
MQ1 =aQ/х1 , MQ2 =bQ/х2;
выражения предельных издержек получим, продифференцировав С=p1x1+p2x2:
MC1=p1, MC2=p2.
Подставим эти выражения в (3.16)
(р0+2 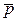 Q*)aQ*/х1* = p1, (р0+2
Q*)aQ*/х1* = p1, (р0+2 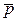 Q*)bQ*/х2*= p2..
Q*)bQ*/х2*= p2..
Откуда можно выразить
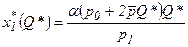 ,
, 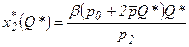 . (3.21)
. (3.21)
Таким образом, определив оптимальный объем производства по формулам (3.19), (3.20), следует затем рассчитать спрос на ресурсы по формулам (3.21).
| Геометрическая интерпретация |
На рис. 3.8 изображены кривые валового дохода R, совокупных издержек С, прибыли П, а также зависимостей предельных и средних значений издержек и дохода. Отличие от вида соответствующих кривых в случае совершенной конкуренции состоит в том, что кривая дохода R имеет уменьшающийся темп роста при увеличении объема производства, и, соответственно, кривая предельного дохода MR является убывающей. Таким образом интерпретируется ситуация монополии. Ситуация монопсонии не приводит к характерным геометрическим отличиям, поскольку вид кривой предельных издержек в общем случае непосредственно не зависит от объема выпуска.
Поскольку при совершенной конкуренции оптимальное значение прибыли достигается при неизменной цене продукции 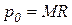 , даже при минимальном объеме выпуска, то в условиях монополии оптимальная величина прибыли всегда не превышает суммы прибыли при совершенной конкуренции:
, даже при минимальном объеме выпуска, то в условиях монополии оптимальная величина прибыли всегда не превышает суммы прибыли при совершенной конкуренции:
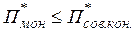
Максимум прибыли в условиях монополии достигается при объеме выпуска, не превышающем оптимальный выпуск в условиях совершенной конкуренции, то есть
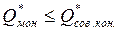 .
.
Пример 3.7.1. Если мукомольный завод (пример 3.3.1), приобретающий зерно по цене 200 руб. за тонну и энергию по цене 300 руб. за килоВтчас, является монополистом, то цена его продукции снижается с ростом продаж р0=10000-2Q (руб. за тонну). Определить оптимальный объем выпуска а) при убывающей отдаче от расширения масштаба (r=0,5), 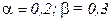 ; б) при отсутствии эффекта расширения масштаба (r=1)
; б) при отсутствии эффекта расширения масштаба (r=1) 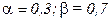 .
.
а) рассчитаем параметр D (см. пример 3.3.1)
 тыс. руб.;
тыс. руб.;
оптимальный объем продукции равен (3.19): 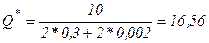 тонн;
тонн;
б) параметр D для данного случая:  тыс. руб.; оптимальный объем продукции (3.20):
тыс. руб.; оптимальный объем продукции (3.20): 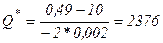 тонн.
тонн.
 |
Рис. 3.8. Оптимальный выпуск в условиях монополии
§3.8. Рациональная коммерческая деятельность
в условиях олигополии и олигопсонии
| Черты олигополии и олигопсонии |
Структура рынка, на котором действует ограниченное количество промышленных организаций, называется конкуренцией среди немногих. Рынок, на котором однородную продукцию предлагают несколько продавцов, называется олигополией. Рынок, на котором продукция определенного вида приобретается несколькими покупателями, называется олигопсонией.
Главная особенность конкуренции среди немногих заключается в том, что все конкурирующие фирмы могут влиять на цены предлагаемой продукции (в случае олигополии) или приобретаемых ресурсов (в случае олигопсонии). Поэтому прибыль каждой коммерческой организации зависит от политики других конкурирующих фирм.
Оптимальная политика каждой коммерческой организации выбирается не только исходя из уровня прямого влияния этой фирмы на состояние рынков ресурсов и продукта, но и с учетом косвенного влияния – через взаимодействие других конкурентов.
Политика организации, действующей в условиях олигополистической конкуренции, имеет много общего с игрой: в обоих случаях прибыль или выигрыш для каждого агента (фирмы или игрока) зависит от действий (расходования ресурсов и выпуска продукции или стратегий) других агентов.
| Задача коммерческой организации |
Наиболее характерным вариантом олигополистической конкуренции является ситуация, в которой два конкурента (дуполия) производят продукцию в соответствии со следующими производственными функциями:
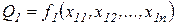 ,
, 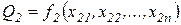 ,
,
где 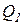 - объем выпуска первой фирмы;
- объем выпуска первой фирмы; 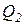 - объем выпуска второй фирмы;
- объем выпуска второй фирмы; 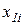 - объем i-го ресурса, затраченный первой фирмой;
- объем i-го ресурса, затраченный первой фирмой; 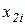 - объем i-го ресурса, израсходованный второй фирмой.
- объем i-го ресурса, израсходованный второй фирмой.
Цена продукции определяется совокупным объемом выпуска:
 ,
,
то есть одновременное повышение объемов производства приводит к снижению результирующей цены:
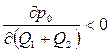
Цены факторов производства определяются объемами закупок соответствующего фактора обеими фирмами:
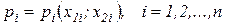 ,
,
то есть если обе фирмы увеличивают объемы приобретения ресурсов, то цены на них возрастают:
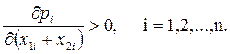
Основная задача одной из конкурирующих коммерческих организаций заключается в максимизации прибыли путем варьирования объемов выпущенной продукции и израсходованных ресурсов:
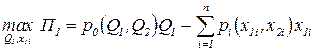 ,
,
при условии
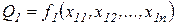 .
.
В данном случае рассматривается формулировка задачи первой из фирм, действующих в условиях олигополистической конкуренции.
| Аналитическое решение |
Функция Лагранжа для сформулированной задачи определения условного экстремума записывается в виде:
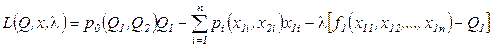 .
.
Условия оптимальности функции Лагранжа первого порядка:
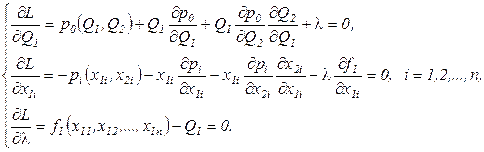 (3.22)
(3.22)
Выразив множитель Лагранжа из первого уравнения системы (3.22) и подставив его выражение вместо  во второе уравнение системы (3.22), можно получить:
во второе уравнение системы (3.22), можно получить:
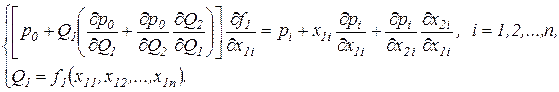
Полученные необходимые условия оптимальности содержат компоненты 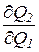 и
и  , которые получили название предположительных вариаций на рынках дуполии и дупсонии, поскольку они отражают предположения первой фирмы относительно возможной реакции конкурента на выбранную ею политику. Выражение
, которые получили название предположительных вариаций на рынках дуполии и дупсонии, поскольку они отражают предположения первой фирмы относительно возможной реакции конкурента на выбранную ею политику. Выражение 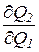 представляет собой изменение объема выпуска продукции второго конкурента при единичном увеличении объема выпуска первого конкурента. Производные
представляет собой изменение объема выпуска продукции второго конкурента при единичном увеличении объема выпуска первого конкурента. Производные  характеризуют изменения затрат ресурса i-го вида второй фирмы при единичном увеличении израсходованного первой фирмой объема данного ресурса.
характеризуют изменения затрат ресурса i-го вида второй фирмы при единичном увеличении израсходованного первой фирмой объема данного ресурса.
Дуполия Курно
| Черты дуполии |
Рассмотрим простейший случай олигополии, в условиях которой действуют два производителя однородного товара (дуполия), производственный процесс которых характеризуется постоянным уровнем предельных издержек, а реализация происходит по линейной модели спроса.
В этом случае функции издержек производителей имеют вид:
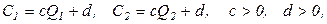
где d – сумма постоянных издержек, с - величина предельных издержек.
Функция предложения товара аддитивна:
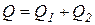 ,
,
а функция спроса может быть представлена в виде:

Функция прибыли одного из дуполистов записывается следующим образом:
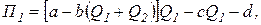 (3.23)
(3.23)
поэтому можно записать условие первого порядка максимизации прибыли:
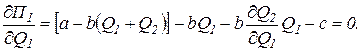
| Гипотеза Курно |
Анализ дуполии Курно[1] основан на предпосылке о том, что предположительные вариации равны нулю, то есть каждый из дуполистов считает, что изменения объема выпуска его продукции не повлияют на объем выпуска продукции конкурента. Равновесие Курно для обеих фирм определяется условиями:
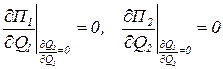 ,
,
или
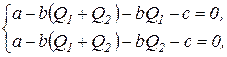 (3.24)
(3.24)
откуда
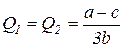 .
.
Соответственно равновесная рыночная цена составит:
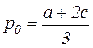 ,
,
а совокупный объем предложения равен:
 .
.
| Обобщение на случай более двух фирм |
Если олигополистическая конкуренция имеет место между F фирмами, то обобщение полученных результатов приводит к выражениям:
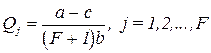 ,
, 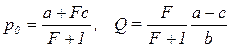 .
.
В условиях неограниченного увеличения числа фирм равновесие Курно стремится к равновесию, характерному для совершенной конкуренции, то есть:
§ индивидуальные объемы производства 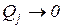 , так как отдельная фирма производит пренебрежимо малое количество продукции;
, так как отдельная фирма производит пренебрежимо малое количество продукции;
§ цена продукции 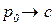 , поскольку отдельная фирма не оказывает влияния на равновесную цену, равную предельным издержкам.
, поскольку отдельная фирма не оказывает влияния на равновесную цену, равную предельным издержкам.
| Геометрическая интерпретация |
Уравнения (3.24) могут быть преобразованы к виду:
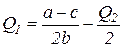 , (3.25)
, (3.25)
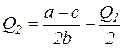 . (3.26)
. (3.26)
Выражения (3.25) и (3.26) называются кривыми реакции дуполистов на поведение друг друга; графически они изображены на рис. 3.9.
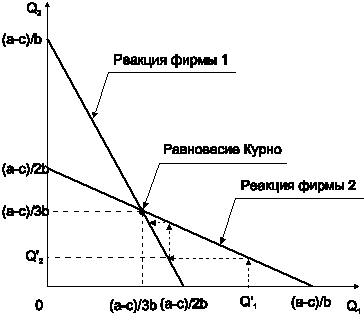
Рис. 3.9. Равновесие Курно
Равновесие достигается на основе взаимодействия реакций дуполистов: например, если в начальный момент времени первая фирма является монополистом, производя Q'1 продукции, то появление второй фирмы с объемом выпуска Q'2 заставит первую снизить объем предложения до Q''1 и т.д.
Поскольку сам процесс достижения равновесия опровергает гипотезу Курно о фиксировании объема выпуска конкурента, то модель Курно не является аутентичной.
Кроме того, сумма прибыли одного дуполиста Курно равна сумме прибыли другого дуполиста (формула (3.23)):
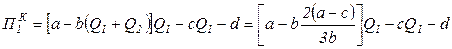 ,
,
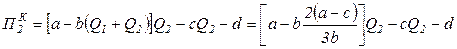 ,
,
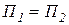 .
.
Таким образом, сумма прибыли каждого из дуполистов Курно составит:
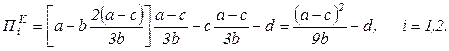 (3.27)
(3.27)
Дата добавления: 2020-10-25; просмотров: 634;











