Интерференция волн. Стоячие волны. Уравнение стоячей волны

Стоячие волны образуются в результате интерференции двух встречных плоских волн одинаковой частоты ω и амплитуды А.

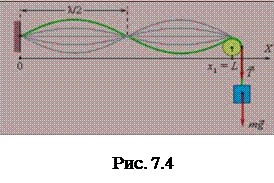
Представим себе, что в точке S (рис.7.4) находится вибратор, от которого вдоль луча SO распространяется плоская волна. Достигнув преграды в точке О, волна отразится и пойдёт в обратном направлении, т.е. вдоль луча распространяются две бегущие плоские волны: прямая и обратная. Эти две волны когерентны, так как рождены одним и тем же источником и, накладываясь друг на друга, будут интерферировать между собой.

Возникающее в результате интерференции колебательное состояние среды и называется стоячей волной.

Запишем уравнение прямой и обратной бегущей волны:

прямая - 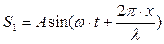; обратная -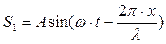

где S₁ и S₂ – смещение произвольной точки на луче SO. С учётом формулы для синуса суммы результирующее смещение равно

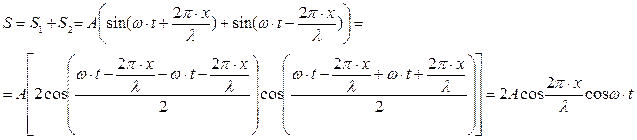
Таким образом, уравнение стоячей волны имеет вид

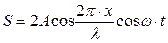(7.17)

Множитель cosωt показывает, что все точки среды на луче SО совершают простые гармонические колебания с частотой 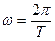. Выражение 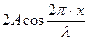называется амплитудой стоячей волны. Как видно, амплитуда определяется положением точки на луче SO (х).

Максимальное значение амплитуды будут иметь точки, для которых

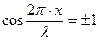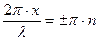или (n = 0, 1, 2,….)

откуда 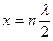, или 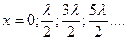(7.18)

Точки, имеющие такие координаты, называют пучностями стоячей волны.

Минимальное значение, равное нулю, будут иметь те точки для которых

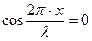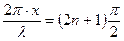или (n = 0, 1, 2,….)

откуда 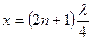или 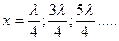(7.19)

Точки, имеющие такие координаты, называют узлами стоячей волны. Сопоставляя выражения (7.18) и (7.19), видим, что расстояние между соседними пучностями и соседними узлами равно λ/2.

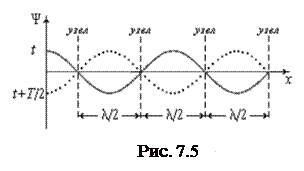На рисунке сплошной линией изображено смещение колеблющихся точек среды в некоторый момент времени, пунктирной кривой – положение этих же точек через Т/2. Каждая точка совершает колебания с амплитудой, определяемой её расстоянием от вибратора (х).

В отличие от бегущей волны в стоячей волне не происходит переноса энергии. Энергия просто переходит из потенциальной (при максимальном смещении точек среды от положения равновесия) в кинетическую (при прохождении точками положения равновесия)в пределах между узлами, остающимися неподвижными.

Все точки стоячей волны в пределах между узлами колеблются в одинаковой фазе, а по разные стороны от узла – в противофазе.

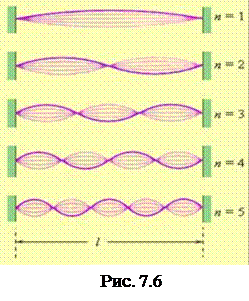
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.

Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.