Коэффициент вариации

Стандартное отклонение – величина именованная, выраженная в тех же единицах измерения, как и средняя арифметическая.

Поэтому для сравнения разных признаков, выраженных в разных единицах измерения, используется не абсолютное, а относительное значение среднего квадратического отклонения в форме коэффициента вариации:

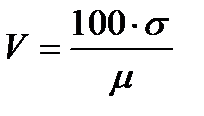, (7.5)

где:

V – коэффициент вариации;

σ – стандартное отклонение;

μ – средняя арифметическая.

Коэффициент вариации есть сигма, выраженная в процентах от средней арифметической. Этот показатель неименованный, поэтому он и пригоден для сравнения разных признаков или одного и того же признака, но в группах с резко различной средней величиной признака.

Пример

Если в стаде коров сводные показатели по удою за первую лактацию равны μ₁ = 3000 кг, σ₁ = 600 кг, а по живому весу μ₂ = 400 кг, σ₂ = 20 кг, то коэффициенты вариации будут иметь следующую величину:

по удою ;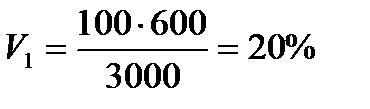

по живому весу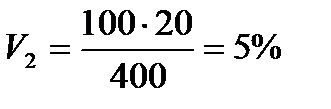

Сопоставление коэффициентов вариации указывает на сильное разнообразие первотелок изученного стада по удою и слабое разнообразие их по живому весу.

В соответствии с этими характеристиками можно заключить, что в исследованном стаде имеются большие возможности отбора по удою (лучших – на племя, худших – на мясо), но слабые перспективы для подобного же отбора по живому весу.

Лимиты и размах

Для быстрой и примерной оценки степени разнообразия часто применяются простейшие показатели:

lim = {min ¸ max} – лимиты, т. е. наименьшее и наибольшее значения признака,

p = (max – min) – размах, или разность между лимитами.

Для группы данных 1, 2, 3, 4, 5 лимиты и размах могут быть обозначены так:

lim = l ¸ 5.

Иногда характеристика разнообразия группы в форме лимитов имеет столь большое производственное значение (например, при упаковке яблок, помидор и т. д., при оценке партии беконных тушек), что кладется в основу денежной оценки продукта.

При проведении параллельных анализов лимиты результатов и их размах служат показателем качества работы лаборанта.

В некоторых случаях лимиты могут служить единственной характеристикой признака.

7.1.4 Приближенные значения μ и s

Если не требуется особой точности, то на основе лимитов можно быстро определить приближенные значения средней арифметической и сигмы.

Средняя арифметическая примерно равна полусумме лимитов:

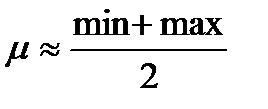. (7.6)

Стандартное отклонение примерно равно разности лимитов, деленной на число K, зависящее от численности группы (n):

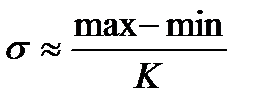(7.7)

Число K можно находить по таблице 7.1.

Таблица 7.1 – Числа K, на которые надо разделить размах значений признака, чтобы получить примерное значение среднего квадратического отклонения

Пример

Среди 20 выловленных волков максимальный вес животного оказался 42 кг, минимальный – 30 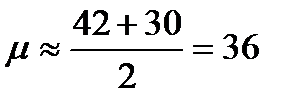кг.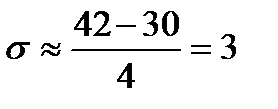

кг; кг.

Перечисленные свойства лимитов и размаха показывают, что эти простейшие показатели разнообразия представляют вполне реальный интерес даже при наличии и более точных показателей.