Средняя геометрическая

Чтобы получить среднюю геометрическую для группы с n данными, нужно все варианты перемножить и из полученного произведения извлечь корень n-й степени:

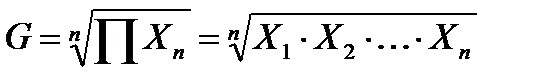, (6.8)

где:

G – средняя геометрическая;

n – число значений;

ΠX_n – произведение вариантов.

Например, средняя геометрическая из 12 и 3 будет равна:

.

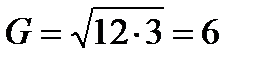Если число значений больше двух, то извлечение корня n-й степени затруднительно, поэтому обычно значение средней геометрической находят путем логарифмирования величин, входящих в основную формулу:

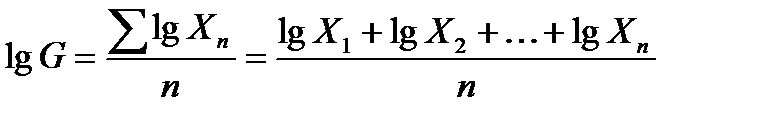. (6.9)

Например, для вариантов 1; 4; 5; 5; 5 среднюю геометрическую можно получить следующим образом:

;

;

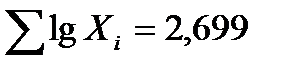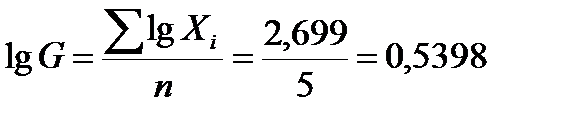G = 3,465.

Для проверки правильности вычисления средней геометрической можно использовать принцип единства суммарного действия. Произведение всех пяти значений ( 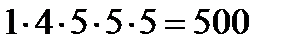) равно произведению пяти выровненных значений, равных средней геометрической:

.

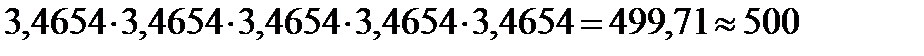Это значит, что средняя в данном случае рассчитана правильно.

Применяется средняя геометрическая во всех случаях, когда необходимо узнать или планировать средние приросты за определенный период. При расчетах среднего попериодного прироста возможны два способа применения средней геометрической.

Первый способ применяется, когда имеются сведения о приростах за каждый период, выраженных в процентах или долях от начала каждого периода. В таких случаях расчет среднего прироста ведется по формуле:

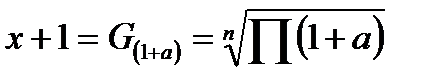, (6.10)

где:

х – средний попериодный прирост за ряд периодов равной продолжительности;

а – фактический прирост за тот или иной период, выраженный в долях;

n – число периодов;

Π(1+а) – произведение величин (1+а).

Из этой формулы следует, что для нахождения среднего прироста по первому способу нужно долю фактического прироста за каждый период прибавить к единице, полученные величины (1+а) перемножить, из их произведения извлечь корень n-й степени и вычесть единицу.

Если периодов много (n > 2), то извлечение корня надо проводить логарифмированием:

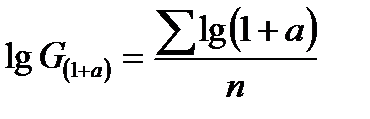. (6.11)

По этой формуле находят логарифмы средней геометрической из величин (1+a), затем находится сама величина G_(1+a) и вычитанием из нее единицы получается искомая средняя доля прироста.

Пример

Поголовье бобров в заповеднике увеличилось за первый год на 5%, за второй – на 20%, за третий – на 50% и за четвертый – на 50%, считая каждый раз от начала истекшего года. Требуется определить среднегодовой прирост за эти 4 года.

Необходимые расчеты приведены в таблице 6.4.

Таблица 6.4 – Расчет среднегодового прироста

Годы	Фактический прирост за каждый год	l + a	lg(l + a)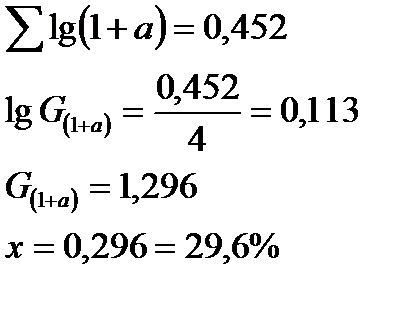
%	доля
		0,05	1,05	0,021
		0,20	1,20	0,079
		0,50	1,50	0,176
		0,50	1,50	0,176

Второй способ расчета средних приростов применяется в тех случаях, когда имеются данные об абсолютных количествах объектов на начало и конец общего большого периода и требуется рассчитать средний прирост за более мелкие периоды.

В таких случаях средний прирост рассчитывается по формуле:

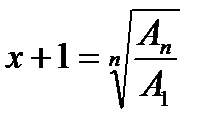. (6.12)

При логарифмировании получаем:

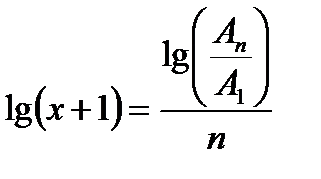, (6.13)

где:

х – средний прирост за более мелкие периоды: среднегодовой за пятилетку, среднемесячный за год, среднесуточный за месяц и т. д.;

А_n – количество объектов на конец общего периода, или, что то же самое, на конец последнего n-го мелкого периода;

А₁ – количество объектов на начало исследуемого общего периода, или, что то же самое, на начало первого мелкого периода.

Пример

На пасеке на начало пятилетки было 100 ульев, а к концу стало 140. Определить среднегодовой процент увеличения пасеки за эту пятилетку. Применяя указанную формулу, получим:

;

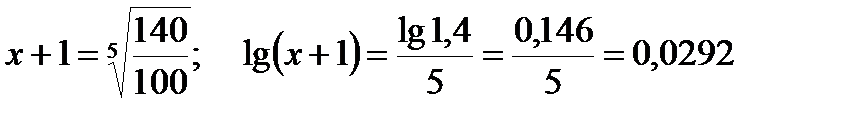x + 1 = 1,0697, x = 0,0697 или 6,97%

Пример

Запланировано за пять лет увеличить производство пенициллина на 60%. Требуется распределить это задание равномерно по годам. В данном случае не даны абсолютные количества в начале и в конце общего периода, но дан общий процент прироста за весь период – 60%, что дает возможность легко получить требуемое отношение 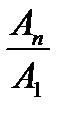. Объем продукции должен увеличиться на 60%. Это значит, что на каждые 100 единиц, бывших в начале общего периода, должно быть 160 единиц в конце:

A_n = 160, A₁ = 100,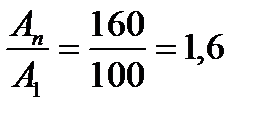

Для выполнения такого задания среднегодовой прирост производства пенициллина можно запланировать следующим образом:

;

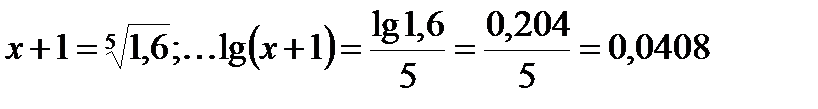х +1 = 1,0985, х = 0,0985, или 9,85 %.

Оказалось, что для увеличения производства за пятилетку на 60% достаточно обеспечить среднегодовой прирост на 9,85%, а не на 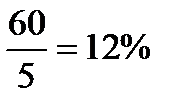, как это могло показаться без учета того, что средний прирост образуется по принципу средней геометрической, а не средней арифметической.