Средняя и сигма суммарной группы
Иногда бывает необходимо определить среднюю и сигму для суммарного распределения, составленного из нескольких распределений. При этом известны не сами распределения, а только их средние и сигмы.
Средняя и сигма в таких случаях находятся по следующим формулам:
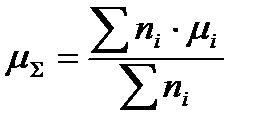 (7.10)
(7.10)
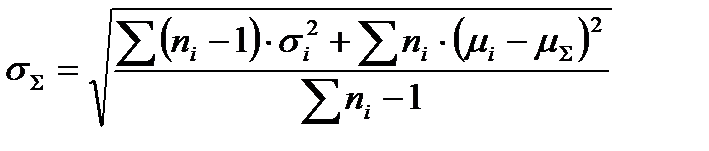 , (7.11)
, (7.11)
где:
ni – численность отдельных объединяемых групп;
μi – средняя арифметическая каждой объединяемой группы;
si – сигма каждой объединяемой группы.
Пример
Четыре независимых наблюдения величины одного и того же вида амеб в сходных условиях дали следующие результаты (в микронах):
| Наблюдения | μ | s | n |
По этим данным средний размер и стандартное отклонение амеб могут быть вычислены, как показано в таблице 7.4.
Разнообразие объектов, составляющих группу, – основное свойство всякой совокупности. Знание закономерностей, по которым формируется разнообразие признака в группе, имеет большое практическое и научное значение.
В малочисленных группах трудно подметить какую–либо закономерность в разнообразии данных. Обычно все значения бывают различны, повторяются без всякой видимой закономерности.
Таблица 7.4 – Вычисление μ и σ суммарной группы
| Исследования | |||||
| ni | 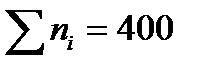
| ||||
| μ i | – | ||||
| si | – | ||||
| ni μi | 
| ||||
| si2 | |||||
| (ni-1) si2 | 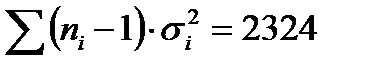
| ||||
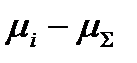
| –1 | + 1 | +1 | ||
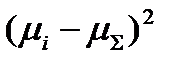
| |||||
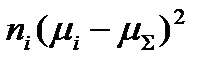
| 
|
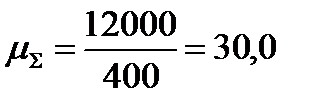 ;
; 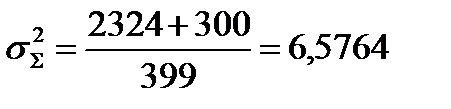 ;
; 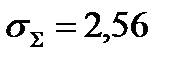 .
.
Дата добавления: 2020-10-25; просмотров: 585;











