Зависимость между случайными величинами

Для исчерпывающей характеристики системы недостаточно знать распределение каждой из величин, входящих в эту систему. Нужно еще знать зависимость между этими величинами. В наиболее общем виде эта зависимость может быть охарактеризована с помощью так называемых условных законов распределения.

Условный закон распределения Х_k – закон распре­деления, определенный при условии, что другие случайные вели­чины X_j (j≠k) приняли заданные значения.

Условный закон распределения можно задавать как функцией F(x_k/x_j, j≠k), так и плотностью распределения f(x_k/x_j, j≠k).Случайные величины, входящие в систему могут быть зависимыми и независимыми

Незвисимые случайные величины –закон распределения каждой из них или любой их подсистемы не зависит от того, какие значения приняли остальные величины.

Функция распределения системы независимых случай­ных величин равна произведению их функций распределения, т.е.

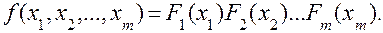
(3.60)

Аналогично плотность распределения системы независимых случайных величин определяется по формуле

(3.61)

Условия, выраженные формулами (3.60) и (3.61), являются необходимыми и достаточными условиями независимости случай­ных величин, входящих в систему.

При наличии линейной связи для характеристики связи двух случайных величин X и У используется второй смешанный цен­тральный момент, называемый корреляционным моментом или мо­ментом связи случайных величин:

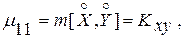
(3.62)

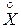где и 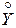—центрированные случайные величины [см. формулу (3.23)]. Для дискретных случайных величин

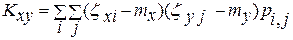
(3.63)

где p_{i, j} = р(Х= x_i, Y= у_j)—вероятность совместного появления событий x_i и y_j.

Если X и У независимые случайные величины, то p_ij = p_ip_j и К_ху, как следует из формулы (3.63), равно нулю.

Для непрерывных случайных величин

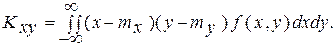
(3.64)

Если X и У независимы, то f(x, у) =f(x)f (у) и, как следует из формулы (3.64), К_Хy=0,

Из формул (3.63) и (3.64) следует, что корреляционный мо­мент характеризует не только линейную зависимость X и У, но и их рассеивание относительно математического ожидания. Так, если одна из величин X или Y очень мало отклоняется от своего математического ожидания, то какой бы тесной ни была связь X и У, корреляционный момент К_ху будет мал. Поэтому для более объективной характеристики связи использу­ется безразмерная характеристика

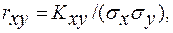
(3.65)

называемая коэффициентом корреляции.

Для независимых случайных величин r_ху = 0 (так как К_ху = 0). Случайные величины, для которых r_ху = 0, называются некоррелированными. Из независимости случайных величин следует их некоррелированность. Из некоррелированности случайных величин их независимость не следует. В случае, если r_xy > 0, говорят о положительной корреляции, если r_ху < 0—об отрицательной. Положительная корреляция между случайными величинами озна­чает, что при возрастании одной из них другая имеет тенденцию к возрастанию; отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию к убыванию.