Статистические характеристики
Имеющиеся ряды наблюдений необходимо представить в наиболее наглядном виде и каким-то образом охарактеризовать. В статистике разработан ряд достаточно простых и наглядных характеристик. При использовании их необходимо иметь в виду, что так как исходные ряды наблюдений являются выборочными, то и их характеристики также должны быть выборочными или статистическими. Естественно, что эти характеристики в той или иной мере могут отличаться от действительных характеристик, полученных по рядам бесконечной продолжительности (см. разд. 3.1).
Статистический ряд
Статистический ряд —первичная форма записи статистического' материала xi ( i=1, 2, . . ., п) в виде таблицы из двух-трех строк или колонок.
В первой строке или колонке таблицы указывают номер члена ряда, во второй — календарный срок или какую-то другую характеристику наблюдений (можно опустить), в третьей — в календарной последовательности располагают значения исходного ряда наблюдений. В табл. 3.1 в качестве примера представлен статистический ряд измеренных значений БПК5 в мг/л
по р. Великой.
Таблица 3.2.
Статистический ряд измеренных значений БПК5 в мг/л
река Великая, г.Псков, верхний створ, за 1995 и 1996 г.
| Номер п/п | Дата | БПК5 | Номер п/п | Дата | БПК5 | Номер п/п | Дата | БПК5 |
| 24.01.95 | 2,1 | 4.08.95 | 3,6 | 3.05.96 | 1,9 | |||
| 22.02.95 | 4,0 | 28.09.95 | 0,8 | 10.06.96 | 3,7 | |||
| 17.03.95 | 3,4 | 30.10.95 | 1,0 | 12.07.96 | 2,1 | |||
| 26.04.95 | 0,9 | 22.11.95 | 1,9 | 21.08.96 | 2.4 | |||
| 25.05.95 | 2,2 | 13.02.96 | 1,2 | 23.09.96 | 1,1 | |||
| 22.06.95 | 1,3 | 29.03.96 | 2,5 | 11.10.96 | 1,0 | |||
| 27.07.95. | 3,0 | 24.04.96 | 0,9 | 13.11.96 | 2,2 |
Для более наглядного представления материала по данным статистического ряда строится график последовательности значений рассматриваемой величины во времени или пространстве. Таким графиком является, например, гидрограф стока (рис. 3.6 ), показывающий изменение стока во времени.
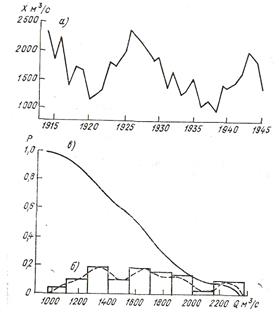
Рис. 3.6. Гидрограф (а), гистограмма (б) и эмпирическая кривая обеспеченности (в) годового стока р. Кама – г. Пермь.
По этому графику можно составить определенное представление
о рассматриваемом процессе: об амплитуде его колебаний, тенденции изменений среднего значения и размаха колебаний, регулярности наблюдений и т.д.
Статистическая совокупность. Гистограмма (статистический многоугольник распределения)
Одной из основных задач статистической обработки материалов наблюдений является определение вероятности того или иного значения или диапазона значений случайной величины. Приближенное представление об этой вероятности можно получить с помощью специальной таблицы. Для построения ее необходимо подсчитать количество наблюдений тj, попадающих в тот или иной заранее заданный j-й интервал (группу) возможных значений данной случайной величины, и рассчитать частоту pj = mj/n попаданий наблюденных величин в каждый j-й интервал, где n – период наблюдений.
Статистическая совокупность – совокупность групп, на которые разбивают значения исследуемой случайной величины, и частот попадания данных наблюдений в каждую группу (табл. 3.3).
Графическое изображение статистической совокупности называется гистограммой или статистическим многоугольником.
Таблица 3.3.
Статистическая совокупность измеренных значений БПК5 в мг/л
река Великая, г.Псков, верхний створ, за период наблюдений с 1995 по 1998 г.
| Группа | 0,6-1,1 | 1,1-1,6 | 1,6-2,1 | 2,1-2,6 | 2,6-3,1 | 3,1-3,6 | 3,6-4,1 |
| m | |||||||
| 0,18 | 0,33 | 0,15 | 0,13 | 0,10 | 0,05 | 0,08 |
Для построения гистограммы по оси абсцисс последовательно откладывают границы групп или интервалов исследуемой величины. На каждом из этих интервалов, как на основании, строят прямоугольник высотой р. Последовательность полученных прямоугольников, сумма высот которых равна 1, и представляет собой гистограмму (см. рис. 3.9.б).
Гистограмма позволяет сделать ряд достаточно определенных предположений об имеющемся ряде наблюдений: об амплитуде колебаний относительно средних значений, о наиболее вероятных значениях, симметричности колебаний относительно среднего значения, характере изменений частоты с изменением длин интервалов значений и т. д.
Согласно теореме Бернули, при неограниченном увеличении числа опытов частота события xi ≤ X < xi+1 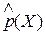 сходится по вероятности к вероятности этого события
сходится по вероятности к вероятности этого события 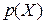 , т. е.
, т. е.
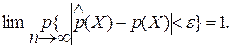
 (3.66)
(3.66)
Отсюда, соединяя точки вершин прямоугольников, соответствующие средним значениям интервалов, получим приближенный график плотности вероятности тем более точный, чем ближе n к N ичем больше количество интервалов взято в расчет.
Следует отметить, что результаты анализа ряда наблюдений по гистограммам в некоторой степени зависят от числа групп или интервалов. Чрезмерное увеличение числа групп при ограниченном материале наблюдений приведет к истощению информации о каждой группе в отдельности и большим погрешностям в определении частоты ее значений. Уменьшение числа групп приведет к излишней схематизации анализа.
На основании имеющегося опыта обычно рекомендуется выбирать число групп таким, чтобы среднее число точек наблюдений в группе было не меньше семи-восьми. Иногда для определения числа групп или интервалов используется формула
K = 5 lg n , (3.67)
где n – число членов ряда.
Дата добавления: 2020-10-25; просмотров: 530;











