РАСЧЕТ И КОНСТРУИРОВАНИЕ ШТАНГОВОЙ КОЛОННЫ

Существующие методы расчета штанговых колонн ориентиро­ваны на конструирование колонн для откачки нефти из условно - вертикальных скважин. В основу методов расчета положен учет напряжений от осевых усилий. Между тем в наклонно направ­ленных скважинах, имеющих участки повышенной кривизны, штанги изгибаются, и, следовательно, в штангах, расположен­ных на этих участках, возникают дополнительные напряжения от изгиба. В отдельных случаях значение напряжений от изгиба сопоставимо со значением напряжений от растяжения, поэтому

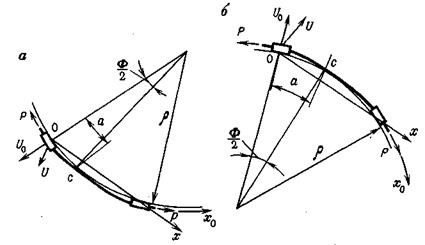
Рис. 32. Схема расположения насосной штанги:

а - на участка кривизны; б - на участке спада кривизны

пренебрежение напряжениями от изгиба при конструировании штанговых колонн для ННС ведет к повышенной частоте обрывов штанг в наклонных скважинах.

В связи с этим ниже приводится метод расчета и конструи­рования штанговых колонн, учитывающий напряжения от изгиба штанг в ННС [24].

Уравнение упруго-деформированной оси колонны штанг жест­костью EIна участке набора или спада зенитного угла сква­жины радиусом R, под действием растягивающих нагрузок Р и поперечных составляющих сил собственного веса колонн ±q*sinα, где α - зенитный угол скважины, имеет вид (рис. 32)

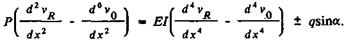(76)

Здесь υ_r - прогиб, соответствующий начальному искривлению

оси скважины в плоскости декартовых координат уох; υ₀ -прогиб оси штанг относительно оси скважины в плоскости у₀ох₀, где ось х совпадает с осью первоначально искривленной оси штанг при отсутствии влияния растягивающих сил Р и по­перечных нагрузок q*sinα, т.е. ось x₀ - параллельна оси скважины и аппроксимируется на рассматриваемом участке колонны в виде дуги окружности радиусом R. Величина υ_r для постоянного радиуса Р на рассматриваемом участке легко получается элементарным геометрическим путем и сводится к виду:

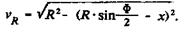(77)

Дифференцируя υ_r получаем:

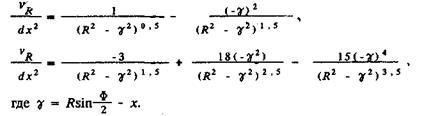
Функцию υ₀ будем аппроксимировать в виде тригонометрической функции

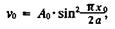(78)

где а - расстояние от муфты до места касания штанговой стенки ствола скважины, а при отсутствии такого касания - до середины расстояния между муфтами. С радиусом кривизны ствола величина а связана соотношением

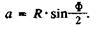
Дифференцируя (78), находим

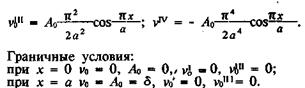
Для реальных систем х = х₀. Наибольший интерес пред­ставляет случай, когда колонна касается стенок скважины на каком-то расстоянии d от муфты. В этом случае

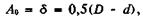
где D - диаметр муфты; d - диаметр штанг по телу.

Следует иметь в виду, что в момент касания штанг длиной l стенки ствола а = l/2, При а > l/2напряжения изгиба в по­перечном сечении штанг также будут определяться по при­веденной ниже формуле (82), но с подстановкой в нее величины l/2вместо d. При этом уже значение A₀≠δ находят из формулы (80) при а = l/2.

Решая уравнение (76) с учетом (77) и (78), получаем выражение, которое при R → ∞ совпадает с классическим при­ближенным решением для защемленных балок, а в рассматри­ваемом случае имеет вид

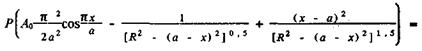
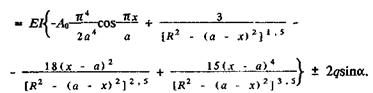(80)

Полученное решение является неявным относительно а, но для реальных систем (а - х)«Rи при х = а A₀= υ_{0 / x-a} =δ

Тогда

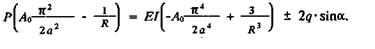
Откуда

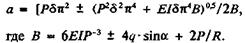(81)

В выражении (81) берется верхний знак +, так как мнимая величина а противоречит физическому смыслу задачи.

Напряжения изгиба σ_н в поперечном сечении штанг от из­гибающего момента М_н имеют максимальное значение в зоне сочленения штанг с муфтами и равны (при х = 0)

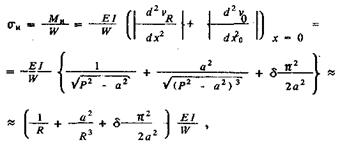
где а определяется из формулы (81).

На рис, 33 представлена зависимость напряжений изгиба от радиуса кривизны ствола скважины при различных значениях осевой нагрузки Р и среднем значении зенитного угла а = 30 . Как видно из представленного графика, пренебрежение влиянием при выборе конструкций штанговых колонн и расчетах на их усталостную прочность или на долговечность недопустимо не только в наклонных скважинах, но и при наличии участков интенсивного локального искривления ствола в вертикальных скважинах (q*sinα = 0).

В отечественной практике для расчета штанговых колонн используют формулу И.А. Одинга

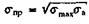
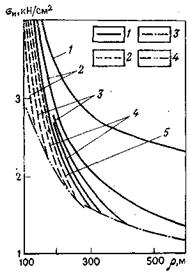
Рис. 33. Напряжение от изгиба штанг в зависимости от радиуса искривления ствола скважины:

1 - на участке спада зенитного угла; 2 - на участке набора; 3, 4 - начало касания стенки НКТ телом штанг, соот­ветственно на участке спада и участке набора

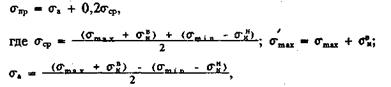
σ_пр, σ_ср - приведенное и среднеарифметическое напряжение цикла соответственно; σ_max, σ_min - соответственно макси­мальное и минимальное напряжение от осевых нагрузок; σ_a- амплитуда изменения напряжения цикла; ( 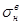, 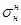- напряжения изгиба в поперечном сечении штанг при ходе вверх и вниз соответственно.

По изложенной методике произведем расчет нагрузок и при­веденных напряжений для трех скважин. Для простоты расчетов, приняв разницу сил инерции между рассматриваемыми случаями несущественной, исключаем их из числа составляющих. Резуль­таты расчетов представлены в табл. 11, 12 и на рис. 34. Анализ результатов показывает, что при искривлении насосных штанг значительно увеличиваются приведенные напряжения, причем чем ближе к дневной поверхности и чем меньше его радиус кривизны, тем больше приведенные напряжения.

В основе рассмотренного расчета, являющегося гипоте­тическим, заложены встречающиеся на практике радиусы ис­кривления. Из примера следует, что при искривлении ствола даже в одном месте традиционный метод конструирования

Таблица11