РАСЧЕТ ГИДРОДИНАМИЧЕСКОГО СОПРОТИВЛЕНИЯ ДВИЖЕНИЮ КОЛОННЫ ШТАНГ

Для расчета сил гидродинамического трения используют известные зависимости, приведенные в работах [3, 9, 13]. Как известно, A.M. Пирвердян получил формулу для расчета сил гидродинамического трения в случае гладкой, т.е. безмуфто­вой штанги и при отсутствии движения жидкости в трубах, а А.Р. Каплан дополнительно учел движение жидкости в трубах со скоростью, соответствующей среднему расходу. М.Д. Валеев экспериментально определил коэффициенты, учитывающие до­полнительное сопротивление, создаваемое штанговыми муфтами.

В ННС штанги в НКТ располагаются эксцентрично. Лами­нарное течение вязкой жидкости между двумя неподвижными эксцентрично расположенными цилиндрами рассмотрено в работе Я.В. Шевелева.

Рассмотрим расчет ламинарного течения в эксцентричном зазоре между штангами и насосными трубами [9]. , Градиент гидростатического давления вдоль скважины равен 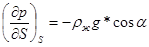, где ρ_ж - плотность жидкости; g - ускорение свободного падения. Градиент давления за счет вязкого сопротивления имеет порядок 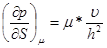, где μ - коэффициент динамической вязкости; v - скорость жид­кости; h - зазор между штангами и трубами. Учитывать вязкое сопротивление нужно, когда оно составляет заметную долю от градиента гидростатического давления, предположим 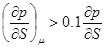. Если исключить из рассмотрения скважины, близкие к горизонтальным, то находим ограничение для значения вязкости .

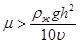Принимая ρ_ж~ 10³/м³; g ~ 10 м/с; h ~ 10 ^–2 м, v ~ 1 м/с, получаем μ > l0^-1 Пa*c.

Для указанных величин находим число Рейнольдса: Re < 100. С другой стороны, известно, что при подъеме жидкости из скважин поток имеет турбулентный характер, когда Re > 10³. Поэтому расчет течения жидкости между штангами и трубами проведем для ламинарного режима.

Опуская динамический и нелинейные члены в уравнении Навье-Стокса, имеем

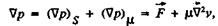
где F - сила тяжести на единицу объема поднимаемой жидкости; v - скорость жидкости; (▼p)_S - (▼p)_μ слагаемые градиента давления, обусловленные силой тяжести и вязкостью.

Введем цилиндрические координаты r, φ, S, связанные с осью скважины. Для проекции первой составляющей градиента давления на ось скважины

(48)

где γ_см = ρ_жg - удельный вес жидкости (смеси).

В выражении для лапласиана пренебрегаем слагаемыми 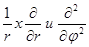. Эти слагаемые тем меньше, чем меньше зазор

между штангами и трубами и чем меньше изменение эксцентри­ситета вдоль колонны. Тогда проекцию слагаемого, обуслов­ленного вязкостью, можно представить в виде

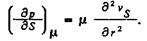(49)

Распределение скорости в кольцевом зазоре между штангами и насосными трубами с учетом граничных условий υ_S (r₀) = υ₀, υ_S (r₀+h) = 0 представим в виде

(50)

где υ₀ - скорость движения штанг: х = r –r₀,;r₀ = D_ш/2, h = h₀(1 – ε*cosφ) - ширина зазора между штангами и трубами; ε = h/h₀ - относительный эксцентриситет.

Если штанги касаются труб, то η = h₀ и ε = 1. Постоянную A определяем из условия сохранения объема жидкости

где Q - расход жидкости через НКТ.

В результате для градиента давления, обусловленного вяз­ким сопротивлением, находим

(51)

где 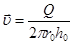- средняя скорость жидкости в кольцевом зазоре между штангами и НКТ.

Изменение давления за счет вязкого сопротивления зависит от эксцентриситета. При максимальном эксцентриситете ε = 1, когда штанги касаются труб, изменение давления в 2,5 раза меньше, чем в концентричном случае. Такой же результат по­лучается при точном решении задачи о течении вязкой жидкости в кольцевом эксцентричном канале по Я.В. Шевелеву.