Теорема об изменении количества движения точки

Количеством движенияматериальной точки называется векторная мера её движения, равная произведению массы точки на её скорость.

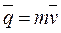
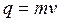
Вектор количества движения по направлению совпадает со скоростью. Количество движения точки можно проецировать на координатные оси, раскладывать на составляющие.

Единицы измерения количества движения – кг∙м/с.

При движении точки величина и направление вектора 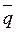изменяются, так как силы, приложенные к точке, приводят к изменению её скорости.

Это изменение можно охарактеризовать элементарным импульсом силы – вектором, равным произведению силы на элементарный (бесконечно малый) промежуток времени её действия.

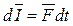
Так как весь промежуток времени состоит из бесконечно большого числа бесконечно малых промежутков, то их сумма перейдёт в интеграл:

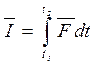
Если сила постоянна, то импульс силы за промежуток времени Δt равен произведению силы на промежуток времени:

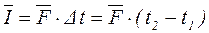
где t₁ и t₂ – конечные и начальные моменты времени.

Пусть на точку массой m действует система постоянных сил, равнодействующая которых 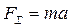. Рассмотрим случай, когда точка движется прямолинейно, a=const, точка движется равномерно.

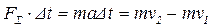
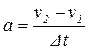
Теорема об изменении количества движения точки: изменение количества движения точки равно импульсу всех внешних сил, действующих на данную точку.

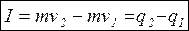
Направление вектора импульса совпадает с направлением вектора силы. Единица импульса в СИ- Н∙с. Если на точку действует несколько сил, то их общий импульс равен геометрической сумме импульсов отдельных сил.