Основное уравнение динамики вращающегося тела

Пусть твёрдое тело под действием внешних сил вращается вокруг неподвижной оси z с угловым ускорением ε.

Вращающий момент – это алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси oz.

Разобьём тело на множество материальных точек с массой Δm_k. При вращении тела каждая из этих точек движется по окружности радиуса R_k с ускорением а_k, которое раскладывается на нормальную и касательную составляющие.

К каждой материальной точке приложим элементарные силы инерции:

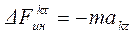
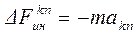
По принципу Даламбера активные силы, реакции связей и силы инерции образуют уравновешенную систему, поэтому алгебраическая сумма моментов всех этих сил относительно оси z должна быть равна нулю.

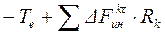
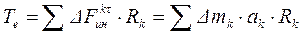
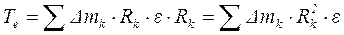Величина 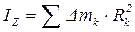называется моментом инерции тела (системы) относительно этой оси. Момент инерции тела равен сумме произведений масс точек на квадрат расстояний до оси вращения.

Основное уравнение динамики вращающегося тела:

Произведение момента инерции тела на его угловое ускорение равно сумме моментов всех сил относительно оси вращения.

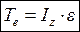
Чем больше момент инерции тела, тем больший вращающий момент следует приложить для сообщения телу определённого условного ускорения. Момент инерции массы можно рассматривать как меру инертности твёрдого тела во вращательном движении, аналогично тому, как масса служит мерой инертности материальной точки или тела при поступательном движении.