Модели долгосрочного страхования жизни

Задача 5.1.Предположим, что продолжительность жизни описывается моделью де Муавра с предельным возрастом 120 лет, а эффективная годовая процентная ставка равна 15%. Подсчитайте нетто-премии для человека в возрасте 40 лет, если заключается договор:

а) пожизненного страхования;

б) 5-летнего смешанного страхования жизни;

в) пожизненного страхования, отсроченного на 2 года;

г) пожизненного страхования с непрерывно увеличивающейся страховой суммой.

Решение.

Как мы знаем, остаточное время жизни застрахованного имеет равномерное распределение на промежутке 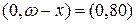, значит, функция плотности имеет вид:

.

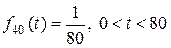Интенсивность процентов 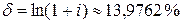, коэффициент дисконтирования 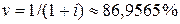. После этих предварительных замечаний приступим к расчетам:

а) для пожизненного страхования имеем

.

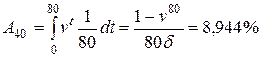б) для смешанного 5-летнего страхования

.

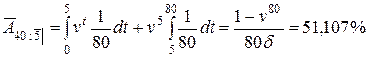в) для пожизненного, отсроченного на 2 года

.

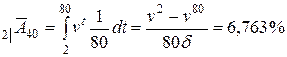г) для пожизненного, с непрерывно увеличивающейся страховой суммой

.

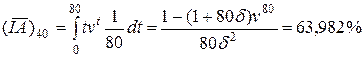Задача 5.2. Страховая компания заключила 10000 договоров пожизненного страхования. Предположим, что остаточное время жизни каждого из застрахованных характеризуется интенсивностью смертность 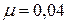, которая не меняется с течением времени, а интенсивность процентов .

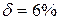Подсчитайте величину премии, которая гарантировала бы 95% вероятность выполнения компанией своих обязательств.

Решение.

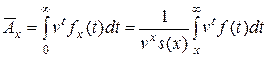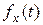Подсчитаем вначале нетто-премию. В соответствии с формулой , где – плотность остаточного времени жизни. Поскольку нам известна интенсивность смертности, то мы можем найти функцию выживания

,

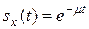что, в свою очередь, дает формулу для плотности :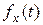

.

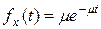Теперь мы можем подсчитать нетто-премию:

.

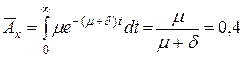Второй момент

,

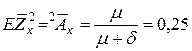следовательно, дисперсия

.

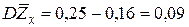Теперь относительная страховая надбавка равна:

.

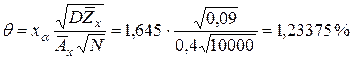Соответственно премия есть

.

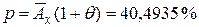Напомним, что величина страховой суммы 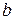используется нами в качестве единицы измерения денежных сумм, так что, если, например, 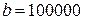рублей, то 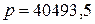рубля.