Модели краткосрочного страхования жизни
Задача 4.1. Предположим, что в компании застраховано 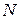 = 3000 человек с вероятностью смерти в течение года
= 3000 человек с вероятностью смерти в течение года 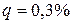 . Компания выплачивает сумму
. Компания выплачивает сумму 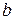 = 250000 руб. в случае смерти застрахованного в течение года и не платит ничего, если этот человек доживет до конца года. Определите величину активов, достаточную, чтобы обеспечить вероятность разорения порядка 5%.
= 250000 руб. в случае смерти застрахованного в течение года и не платит ничего, если этот человек доживет до конца года. Определите величину активов, достаточную, чтобы обеспечить вероятность разорения порядка 5%.
Решение.
Примем размер страховой суммы в качестве новой денежной единицы.
Прежде всего, мы должны подсчитать среднее значение и дисперсию суммарного ущерба 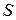 .
.
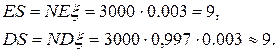
Поэтому
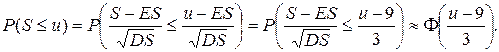
Если мы хотим, чтобы вероятность разорения была 5%, величина 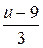 должна быть равной
должна быть равной 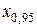 = 1,645, т.е.
= 1,645, т.е. 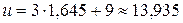 (от величины страхового пособия) или в абсолютных цифрах около 3 483 750 руб.
(от величины страхового пособия) или в абсолютных цифрах около 3 483 750 руб.
Задача 4.3. Страховая компания предлагает договоры страхования жизни на один год. Информация относительно структуры покрытия приведена в следующей таблице:
| Страховая сумма | Причина смерти | Вероятность |
| 500 000 | Обычная | 0,1 |
| 1 000 000 | Несчастный случай | 0,01 |
Относительная защитная надбавка равна 20%.
Предположим, что отдельные полисы независимы и страховщик использует нормальное приближение для распределения суммарных выплат.
Сколько договоров должен продать страховщик, чтобы собранная премия с вероятностью 95% покрывала суммарные выплаты?
Решение.
Пусть 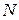 – общее число проданных договоров.
– общее число проданных договоров. 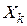 – выплаты по
– выплаты по 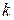 -му договору,
-му договору, 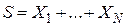 – суммарные выплаты по всему портфелю,
– суммарные выплаты по всему портфелю, 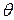 – относительная защитная надбавка, так что премия по одному договору равна
– относительная защитная надбавка, так что премия по одному договору равна 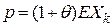 .
.
По условию, 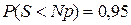 . С другой стороны,
. С другой стороны,
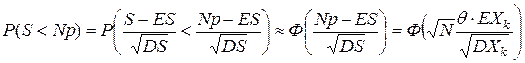 .
.
Поэтому
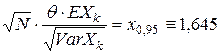 ,
,
где 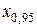 – квантиль порядка 0,95 стандартного нормального (гауссовского) распределения.
– квантиль порядка 0,95 стандартного нормального (гауссовского) распределения.
Отсюда для искомого числа договоров имеем:
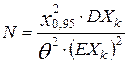 .
.
Поскольку для индивидуального договора,
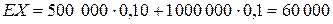 ,
,
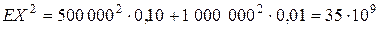 ,
,
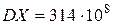 , искомое число договоров равно 590.
, искомое число договоров равно 590.
Дата добавления: 2020-10-14; просмотров: 461;











