Приближенный расчет вероятности разорения

Обычно число застрахованных в страховой компании очень велико. Поэтому подсчет вероятности разорения предполагает расчет функции распределения суммы большого числа слагаемых. В этом случае применение ЭВМ может привести к проблемам, связанным с малостью вероятностей. Однако обстоятельство, затрудняющее точный расчет, открывает возможность быстрого и простого приближенного расчета. Это связано с тем, что при росте 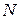вероятность 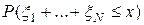часто имеет определенный предел (обычно нужно, чтобы 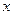определенным образом менялось вместе с 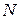), который можно применять в качестве приближенного значения искомой вероятности. Точность подобных приближений обычно очень велика и удовлетворяет практические потребности. Основным является нормальное (или гауссовское) приближение.

Гауссовское приближение основано на центральной предельной теореме теории вероятностей. В простейшей формулировке эта теория выглядит следующим образом:

если случайные величин 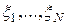независимы и одинаково распределены со средним 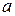и дисперсией 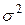, то при 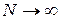функция распределения центрированной и нормированной суммы

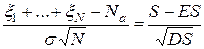
имеет предел, равный

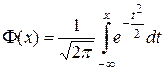
Поэтому, если число слагаемых велико, то можно написать приближенное равенство:

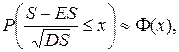
или, что то же самое,

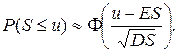
Существуют многочисленные обобщения центральной теоремы на случаи, когда слагаемые 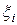, имеют разные распределения, являются зависимыми и т.д. Детальное обсуждение этого вопроса увело бы нас слишком далеко в сторону от изучаемого предмета. Поэтому мы ограничимся утверждением, что если число слагаемых велико (обычно достаточно, чтобы 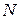имело бы порядок нескольких десятков), а слагаемые не очень малы, то применимо гауссовское приближение для нахождения вероятности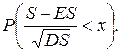

Конечно, это утверждение очень неопределенно, но и классическая центральная предельная теорема без точных оценок погрешности не дает ясного указания на сферу применения.

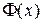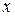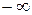Функция при росте от до 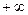возрастает от 0 до 1 и непрерывна. Поэтому она может рассматриваться как функция распределения некоторой случайной величины 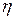. Это распределение называется гауссовским, или нормальным. Оно не зависит от каких-либо параметров и детально изучено в теории вероятностей. Существуют подробные таблицы как для функции распределения 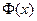, так и для плотности.

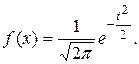
Значения 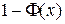в наиболее интересном диапазоне 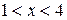приведены в следующей таблице:

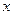
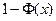
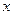
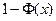
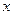
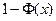
1.0	15.87%	2.0	2.28%	3.0	0.135%
1.1	13.57%	2.1	1.79%	3.1	0.097%
1.2	11.51%	2.2	1.39%	3.2	0.069%
1.3	9.68%	2.3	1.07%	3.3	0.048%
1.4	8.08%	2.4	0.82%	3.4	0.034%
1.5	6.68%	2.5	0.62%	3.5	0.023%
1.6	5.48%	2.6	0.47%	3.6	0.020%
1.7	4.46%	2.7	0.35%	3.7	0.011%
1.8	3.59%	2.8	0.26%	3.8	0.007%
1.9	2.87%	2.9	0.19%	3.9	0.005%

Полезно также иметь таблицу квантилей 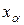, отвечающих достаточно малой вероятности разорения :

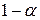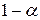
	1%	2%	3%	4%	5%
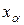
	2.33	2.05	1.88	1.75	1.645