Зразок виконання задачі 2
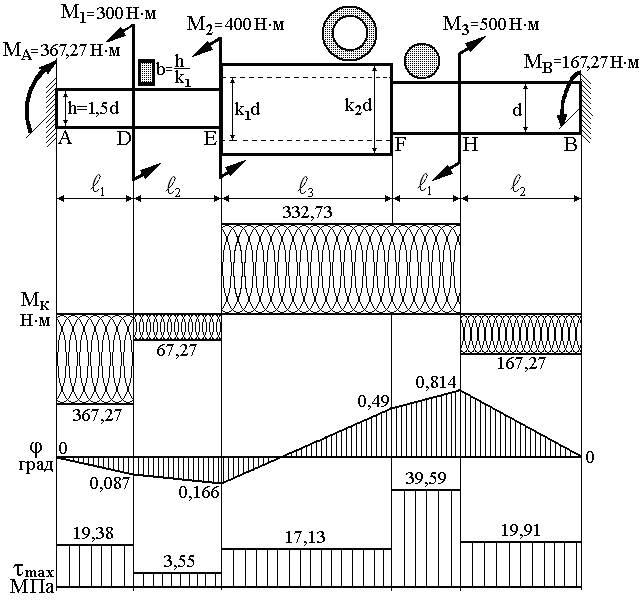
З умов міцності та жорсткості визначити розміри поперечних перерізів статично невизначуваного стержня з послідовним розташуванням ділянок прямокутного, кільцевого та круглого перерізів (рис. 3.16).
Дано:
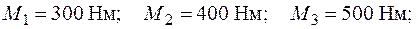
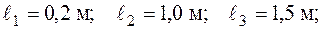
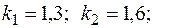
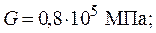
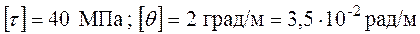 .
.
1. Визначимо геометричні характеристики поперечних перерізів ділянок стержня:
– кільцевий переріз:
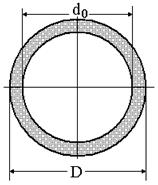
| 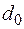 – внутрішній діаметр; – внутрішній діаметр; 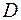 – зовнішній діаметр; – зовнішній діаметр;
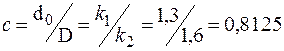 .
Полярний момент інерції: .
Полярний момент інерції:
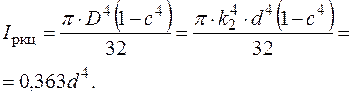
|
Полярний момент опору:
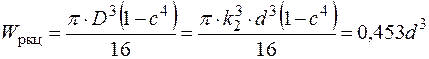 .
.
– круглий переріз:
| Полярний момент інерції:
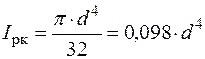 .
Полярний момент опору: .
Полярний момент опору:
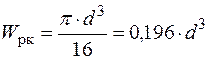 . .
|
– прямокутний переріз: 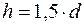 ;
; 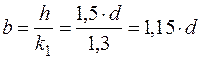 .
.
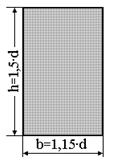
| Момент інерції при крученні: 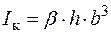 , ,
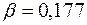 залежить від співвідношення сторін прямокутника залежить від співвідношення сторін прямокутника 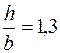 ; (див. табл. 3.1). ; (див. табл. 3.1).
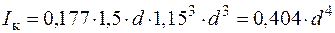 . .
|
Момент опору при крученні ( 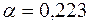 , див. табл. 3.1)
, див. табл. 3.1)
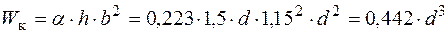 .
.
|
| Рисунок 3.16 |
2. Розкриємо статичну невизначуваність задачі.
При даному типі навантаження в місцях закріплення вала виникають два реактивні моменти 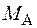 та
та 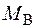 в площинах, перпендикулярних до осі стержня. Ступінь статичної невизначуваності
в площинах, перпендикулярних до осі стержня. Ступінь статичної невизначуваності 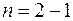 дорівнює одиниці, тому задача є один раз статично невизначувана.
дорівнює одиниці, тому задача є один раз статично невизначувана.
Статичний аспект задачі:
З умови рівноваги вала:
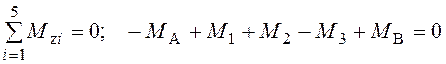 . (3.17)
. (3.17)
Геометричний аспект задачі:
Заміняємо початкову статично невизначувану задачу на статично визначувану, умовно відкидая ліву опору. На підставі принципу незалежності дії сил абсолютний кут закручування лівого краю стержня відносно нерухомого правого дорівнює алгебраїчній сумі кутів закручування від кожного зовнішнього моменту:
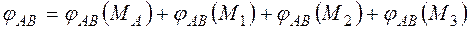
Оскільки обидва кінці валу жорстко закріплені, то кут повороту переріза А відносно В дорівнює нулю (рівняння сумісності кутів закручування):
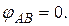 (3.18)
(3.18)
Фізичний аспект задачі:
Використовуючи формулу закону Гука, запишемо вирази для кутів закручування:
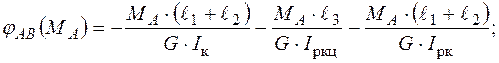
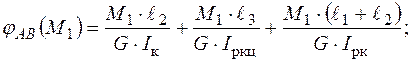
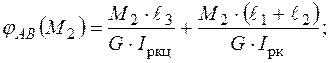 (3.19)
(3.19)
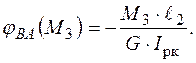
Якщо підставити вирази (3.19) у вираз (3.18), то матимемо:
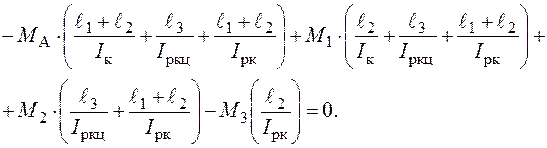 (3.20)
(3.20)
Із рівняння (3.20) знаходимо значення 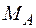 .
.
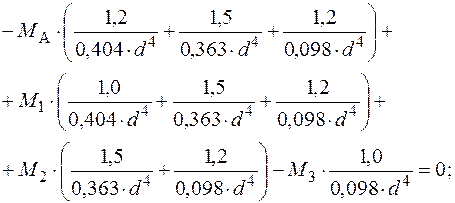
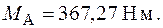
З рівняння рівноваги (3.17) знаходимо значення реактивного моменту 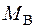 :
:
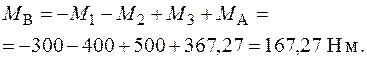
3. Будуємо епюру крутних моментів (рис. 3.16).
4. Визначаємо значення параметру 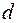 для заданих форм поперечних перерізів стержня з умови міцності:
для заданих форм поперечних перерізів стержня з умови міцності:
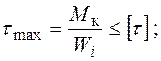
для кільцевого перерізу з епюри крутного моменту (рис. 3.16) 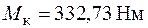 , тоді
, тоді
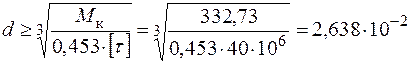 м;
м;
для круглого перерізу ( 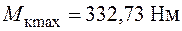 )
)
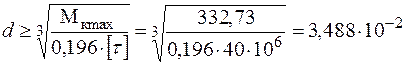 м;
м;
для прямокутного перерізу ( 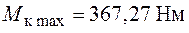 )
)
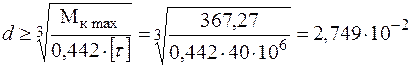 м.
м.
З трьох отриманих результатів слід вибирати більший: 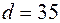 мм, який знайдено з умови міцності для круглого перерізу.
мм, який знайдено з умови міцності для круглого перерізу.
5. Будуємо епюру розподілу максимальних дотичних напружень по довжині стержня: для круглого перерізу 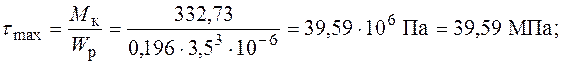
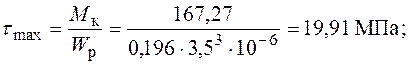
для кільцевого перерізу
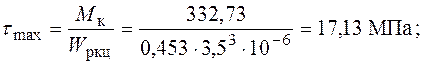
для прямокутного перерізу
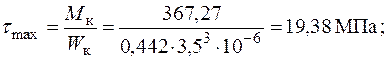
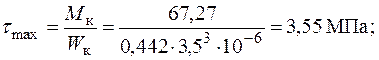
6. Побудуємо епюру кутів закручування.
Послідовно для частин стержня знаходимо значення кутів закручування.
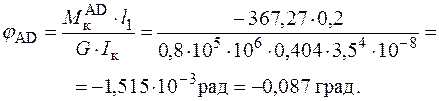
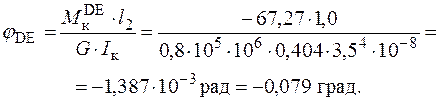
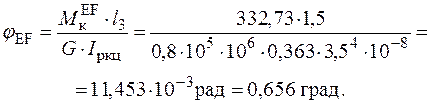
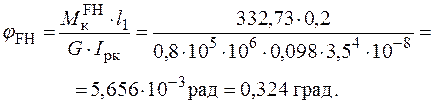
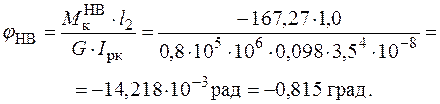
Перевіримо виконання умови жорсткості для найнебезпечнішої ділянки FH круглого перерізу, де відносний кут закручування дорівнює:
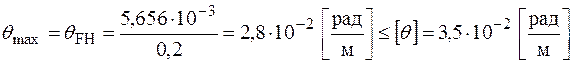 .
.
Умова жорсткості виконана.
Встановимо початок координат у перерізі A та будуємо епюру кутів закручування для деформаційної перевірки: 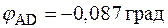 ;
;
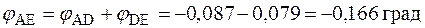 ;
;
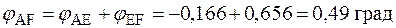 ;
;
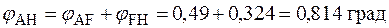 ;
;
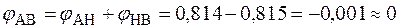 .
.
Абсолютний кут закручування перерізу А відносно перерізу В повинен дорівнювати нулю. Але отримана абсолютна похибка (0,001) є результатом накопичення округлення на кожному етапі рішення задачі. Тому визначимо відносну похибку обчислень 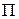 та порівняємо з її допустимим значенням:
та порівняємо з її допустимим значенням:
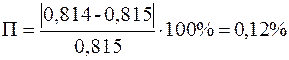 << 5%,
<< 5%,
що свідчить про точність отриманих результатів та правильність рішення статично невизначуваної задачі.
Дата добавления: 2020-10-14; просмотров: 588;











