Диференціальні залежності при згинанні

Розглянемо балку, навантажену довільним розподіленим навантаженням q(z) (рис. 2.6 а). В перерізі на відстані 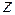виділимо елемент довжиною dz . В перерізі I діють внутрішні силові фактори і , в перерізі II на відстані від першого діють внутрішні зусилля 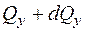і + . У межах нескінченно малого dz навантаження q(z) можна вважати рівномірно розподіленим та рівним q.

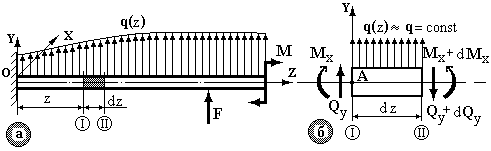
Рисунок 2.6

Оскільки балка під дією зовнішнього навантаження знаходиться в рівновазі, то і кожен її елемент під дією зовнішніх та внутрішніх зусиль також знаходиться в рівновазі (рис. 2.6 б).

Запишемо рівняння статики:

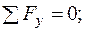
1. 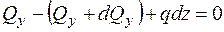, отже

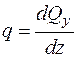(2.1)

2. 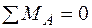; 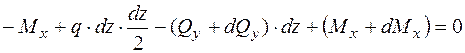, приводячи подібні члени та зневажаючи нескінченно малими другого порядку, одержимо: 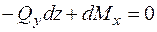, звідки:

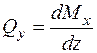. (2.2)

3. Підставимо вираз (2.2) у залежність (2.1), одержимо :

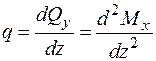. (2.3)

2.1.4. Приклади побудови епюр поперечних сил та

згинальних моментів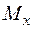

Приклад 1.

Розглянемо консольну балку з рівномірно розподіленим навантаженням q (рис. 2.7). Показуємо поточний переріз з координатою 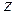, межі її зміни, записуємо функції і . Рівномірно розподілене навантаження q замінюємо зосередженою силою ( 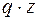), яку прикладено посередині ділянки (плече зосередженої сили 0,5∙z).

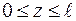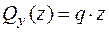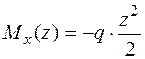Þ ; . Далі обчислюємо значення і : ; ; ; .

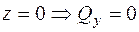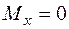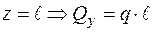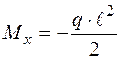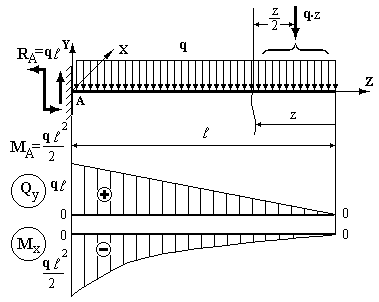
Рисунок 2.7

З побудованих епюр, використовуючи правила перевірки, визначаємо опорні реакці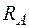ї і 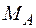. Реакція 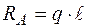дорівнює величині стрибка на епюрі в цьому перерізі та спрямована нагору, тому що позитивна. З умов статики одержуємо те ж саме значення .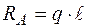

На епюрі в затиcненні скачок моменту дорівнює , отже

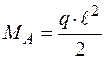. Через те що 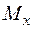в затисненні негативний, то 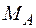повинний бути спрямований проти годинникової стрілки. З умови статики 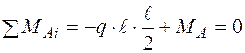одержуємо те ж саме значення: .

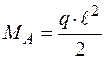Приклад 2.

Розглянемо двохопорну однопролітну балку з рівномірно розподіленим навантаженням q (рис. 2.8).

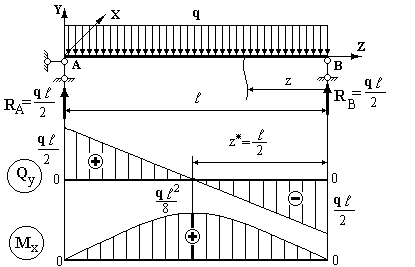
Рисунок 2.8

1. Визначаємо опорні реакції.

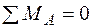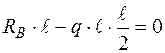, , звідки: .

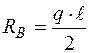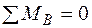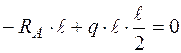, , звідки: .

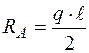Перевірка: , .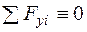

Те, що реакції однакові та рівні половині зовнішнього навантаження, є наслідком симетрії задачі.

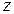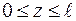2. Показуємо поточний переріз з координатою , межі її зміни та записуємо функції і : Þ ;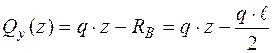

.

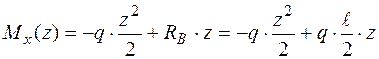Далі обчислюємо значення і :

, .

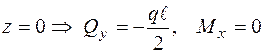Звертаємо увагу, що в точці, де 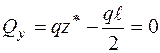, згинальний момент повинен мати екстремальне значення. Таким чином, при .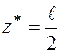

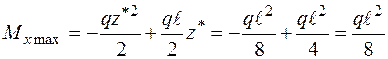Приклад 3.

Розглянемо двохопорну однопролітну балку, яка симетрично навантаженадвома зосередженими силами F (рис. 2.9).

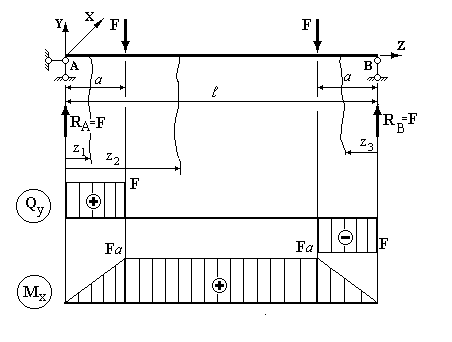
Рисунок 2.9

У зв’язку з симетрією задачі 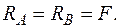Запишемо функції і визначимо характерні значення і для ділянок:

перша ділянка: 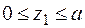Þ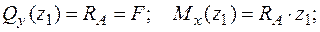

.

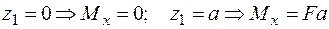друга ділянка: 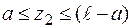Þ ,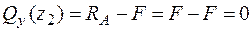

.

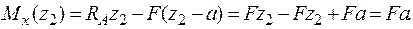Поперечна сила на ділянці дорівнює нулю, отже 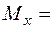const, ділянка зазнає чисте згинання.

третя ділянка: 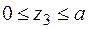Þ ;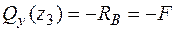

.

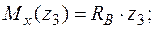
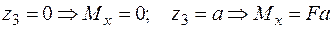Приклад 4.

Розглянемо двоконсольну балку (рис. 2.10).

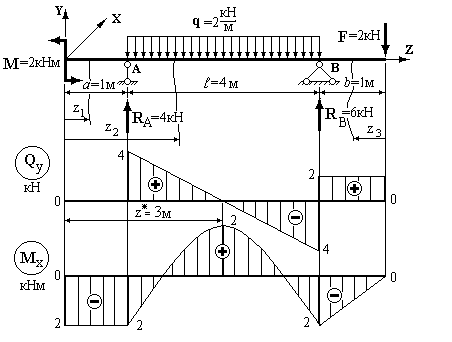
Рисунок 2.10

1. Визначаємо опорні реакції:

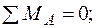
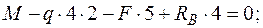звідки 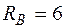кН.

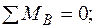
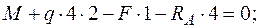звідки 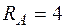кН.

Перевірка: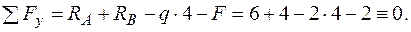

2. Побудуємо епюри внутрішніх зусиль. Для цього розбиваємо балку на ділянки, показуємо перерізи на кожній з них, вказуємо межі зміни координати 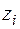, визначаємо й обчислюємо функції і .

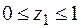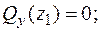
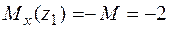Перша ділянка: Þ кНм.

Друга ділянка: 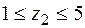Þ

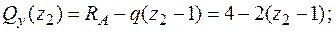
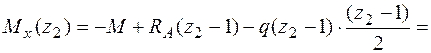
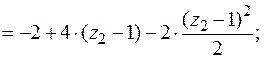
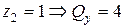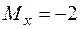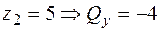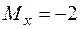кН; кНм; кН; кНм.

На другій ділянці поперечна сила змінює знак, а згинальний момент досягає максимального значення при . Координата 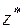визначиться з умови:

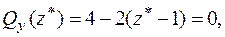звідки 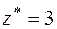м,

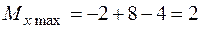кНм.

Третя ділянка: 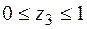Þ

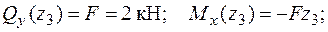
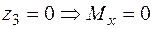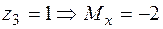; кНм.

2.1.5. Правила побудови та перевірки епюр і

Вищенаведені приклади та диференціальні залежності (2.2) і (2.3) дозволяють установити закономірності розподілів поперечних сил та згинальних моментів по довжині балки.

1. На ділянках, де розподілене навантаження відсутнє ( 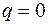), епюра постійна, а епюра представляє лінійну функцію (рис. 2.9).

2. На ділянках з рівномірно розподіленим навантаженням 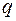епюра лінійна, а епюра − квадратична парабола, причому опуклість парабо-ли спрямована в протилежну сторону дії розподіленого навантаження (рис. 2.7). У точці 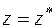, де поперечна сила 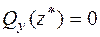(змінює знак), момент досягає екстремального значення ( 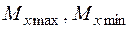) (рис. 2.8).

3. На ділянках, де 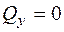, епюра постійна.

4. На ділянці, де поперечна сила позитивна, епюра моменту зростає, і убуває – якщо негативна (у випадку руху зліва направо).

5. У перерізі, де до балки прикладена зосереджена сила F:

· на епюрі спостерігаєтьсястрибок на величину F у напрямку прикладеної сили;

· на епюрі з'являється злам, причому вістря зламу спрямоване проти дії зосередженої сили.

6. У перерізах, де до балки прикладено зосереджений момент, на епюрі спостерігається стрибок на величину цього моменту.