Жорстко закріплений стержень під дією зосередженої сили

Жорстко закріплений обома кінцями стержень площею поперечного перерізу 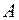навантажений силою 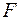(рис. 1.5). Модуль пружності матеріалу 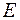. Визначити опорні реакції та побудувати епюру поздовжніх сил.

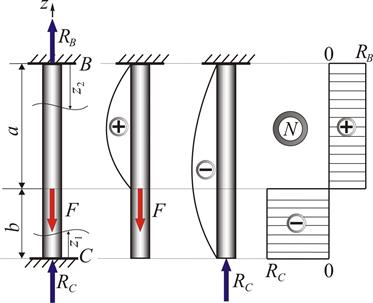
Рисунок 1.5

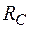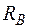1. ССЗ. Показуємо опорні реакції і . Записуємо єдину умову рівноваги, яку можна скласти для даної задачі

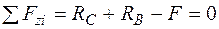. (1.6)

Це рівняння має дві невідомі, тому ступінь статичної невизначеності дорівнює: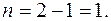

2. ГСЗ. Так як опори жорсткі, то повне подовження стержня дорівнює нулю, тобто 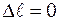. Один з підходів реалізації цієї умови такий. Відкидаємо одну з опор та послідовно прикладаємо зовнішні сили і невідому реакцію у відкинутій опорі. Повне подовження стержня зобразиться як сума подовжень від зовнішнього навантаження 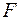− ( 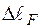) і реакції :

.

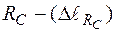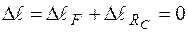3. ФСЗ. Подовження від зовнішнього зусилля у розглянутому випадку складає: 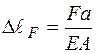, укорочення від реакції: .

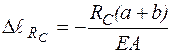4.Синтез. Повна деформація стержня виявляється рівною:

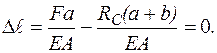(1.7)

З рівняння (1.7) одержуємо 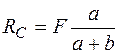, а з рівняння (1.6) випливає: 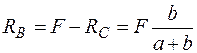. Розбиваємо стержень на дві ділянки та записуємо значення поздовжньої сили на кожній ділянці:

1^а ділянка: 0 £ z₁£ b : ;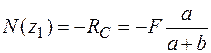

2^а ділянка: 0 £ z₂£ a : .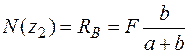

По отриманим рівнянням будуємо епюру поздовжніх сил.