С аргументом Ua при 3-х температурах. Ось абсцисс в Вольтах, ось ординат в Амперах. Для температуры 2420 K построен график Ia2 для обеих ветвей эмиссионного уравнения.

Эмиссионное уравнение способно создавать двухмерный процессовый переход, делая процессы взаимно комплиментарными. Внешняя экспоненциальная «эмиссионная» функция очень чувствительна к масштабам внутренних функций (процессов ).

Потому процессорные переходы, в зависимости от масштабов функций получаются не одинаковыми. Мало того, при моделировании возникает ряд эффектов. Возможно, что в вопросах моделирования процессового перехода с помощью эмиссионного уравнения, требуется новый математический аппарат.

Само «эмиссионное» уравнение можно обнаружить при исследовании вольт-амперных характеристик кремниевых полупроводниковых диодов, при условии изменения температуры.

Это же уравнение успешно моделирует комплиментарные процессы эксперимента С. Дэшмана при исследовании электровакуумного диода. Здесь оно является внешним. Как мы видели, внешних функций для моделирования комплиментарных процессов может быть много. С точки зрения физики, внешней функцией могут быть какие-либо силовые поля, представляемые функцией, которые накладывают свой отпечаток на тепловой и электрический процессы, происходящие в вакуумном диоде с вольфрамовым катодом (силы теплопередачи).

Рассмотрим несколько математических примеров, в которых создаются комплиментарные процессы с применением «эмиссионного» уравнения как внешней функции. Зададим функции-процессы:

y = A = F1(x₀) = x₀² - функция первого процесса

y = B = F2(z₀) = 0,2∙z₀ +50 - функция второго процесса

y _рез = exp( K₁∙ ( K₂∙z - (x-x₀) ∙ (z-z₀) ) )

x₀ = у^1/2 - обратная функция первого процесса.

z₀ = (y – 50)/ 0,2 - обратная функция второго процесса.

Зададим коэффициенты, регулирующие кривизну участка перехода между процессами.

К₁ = 100

К₂ = 0,1

Далее следует:

y = A = F1(x₀) = x₀² - функция первого процесса

y = B = F2(z₀) = 0,2∙z₀ +50 - функция второго процесса

y _рез = exp( -100∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 0,1∙z))

Разработаем алгоритм подпрограммы Midi2_4.

procedure MidI2_4(x,z:real;var y:real;var c0:integer);

var

Ymax, Ymin, X0, E: real;

Kt,Ub,Uf,Tf:real;

A,B,C:real;

begin

c0:=0;

E:=0.000001;

Ymax:= 0.2*z+50 ; // прямая функция для z

Ymin:=0;

Kt:=100;

repeat

begin

y:=(Ymax+Ymin)/2;

Tf:= (y-50)/0.2; // обратная функция для z

Ub:= power( y , (1/2));

Uf:=Ub+0.1;

if y<=0 then

begin

c0:=1;

break;

end;

A:=Ln(y);

B:= ( Ln(y)/Kt+Tf*Ub-z*Uf);

C:= (Tf-z);

if C=0 then

begin

c0:=2;

break;

end;

X0:= B/C;

//X0:=( Ln(y)/Kt+Tf*Ub-z*Uf) / (Tf-z) ; // формула расчета для x

if X0 > x then Ymax:=y else Ymin:=y;

end until (X0+E > x) and (X0-E < x);

end;

На рисунке 5.24. показан график, иллюстрирующий двухмерный процессовый переход. Для процессов y = A = F1(x₀) = x₀² , и

y = B = F2(z₀) = 0,2∙z₀ +50 построена функция

y _рез = exp( -100∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 0,1∙z)) с аргументом x при трёх значениях z = 10, z = 20 и z= 30.

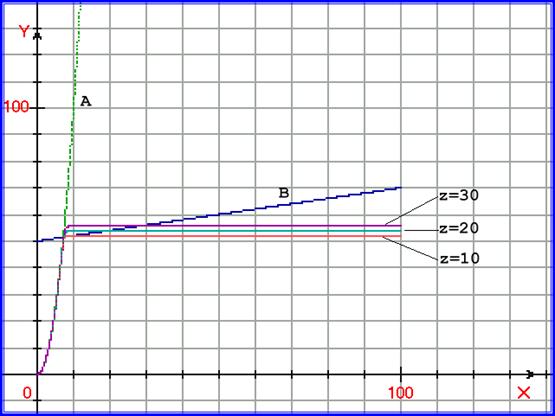
Рис. 5.24.. График, иллюстрирующий двухмерный процессовый переход. Для процессов y = A = F1(x₀) = x₀², и y = B = F2(z₀) = 0,2∙z₀ +50 построена функция

y _рез = exp( -100∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 0,1∙z)) с аргументом x при трёх значениях z = 10, z = 20 и z = 30.

На рисунке 5.25. показан график, иллюстрирующий двухмерный процессовый переход. Для процессов y = A = F1(x₀) = x₀² , и

y = B = F2(z₀) = 0,2∙z₀ +50 построена функция

y _рез = exp( -100∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 0,1∙z)) с аргументом z при трёх значениях x = 7,5 , x = 7,8 и x = 8,1.

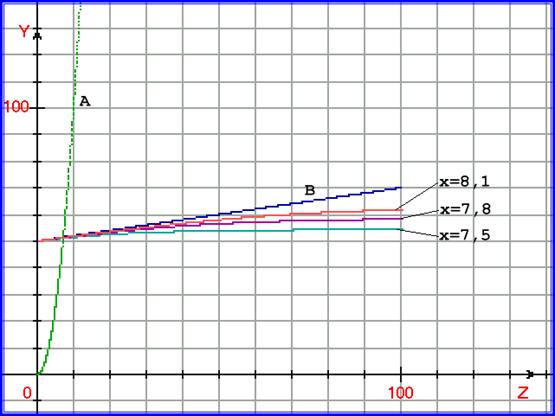
Рис. 5.25.. График, иллюстрирующий двухмерный процессовый переход. Для процессов y = A = F1(x₀) = x₀², и y = B = F2(z₀) = 0,2∙z₀ +50 построена функция

y _рез = exp( -100∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 0,1∙z)) с аргументом z при трёх значениях x = 7,5 , x = 7,8 и x = 8,1 .

Некоторые сочетания:

К₁ = 1

К₂ = 0,01

Для тех же процессов приводят к некорректным вариантам эмиссионного уравнения.

На рисунке 5.26. приведен график такого процессового перехода:

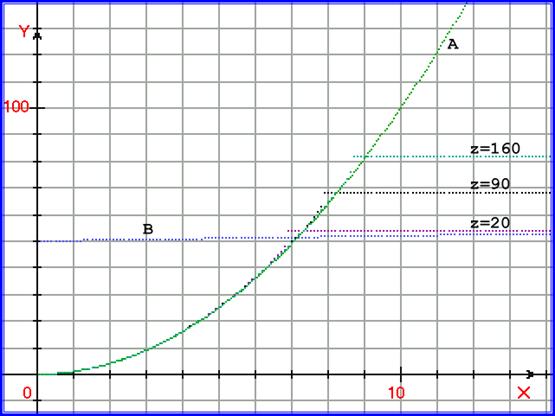
Рис. 5.26. График, иллюстрирующий двухмерный процессовый переход. Для процессов y = A = F1(x₀) = x₀², и y = B = F2(z₀) = 0,2∙z₀ +50 построена функция

y _рез = exp( -1∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 0,01∙z)) с аргументом x при трёх значениях z = 20, z = 90 и z = 160.

Другое сочетание коэффициентов:

К₁ = 100

К₂ = 1

Для тех же процессов приводят к вариантам эмиссионного уравнения, где графики пересекаются в одной точке.

На рисунке 5.27. приведен график такого процессового перехода:

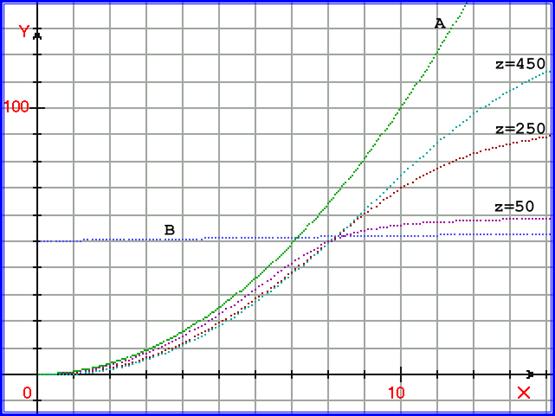
Рис. 5.27. График, иллюстрирующий двухмерный процессовый переход. Для процессов y = A = F1(x₀) = x₀², и y = B = F2(z₀) = 0,2∙z₀ +50 построена функция

y _рез = exp( -100∙ ( (x - у^1/2) ∙ (z - (y – 50)/ 0,2 ) – 1∙z)) с аргументом x при трёх значениях z = 50 , z = 250 и z = 450 .