Примеры моделирования результирующей функции, для двух процессов, ограничивающих рост друг друга при эмиссионном уравнении, в качестве внешней функции.

Рассмотрим одну ошибку алгоритма подпрограммы Midi2_012 – «неправильную точку входа» и как она отражается на воспроизведении «эмиссионного уравнения».

Если в подпрограмме сменим строку входа:

Ymax:=exp( (z-0.01)*0.01047-27.325 ); // прямая функция для z

На строку:

Ymax:=1;

Получим следующий текст:

procedure MidI2_012(x,z:real;var y:real;var c0:integer);

var

Ymax, Ymin, X0, E: real;

Kt,Ub,Ud,Uf,Tf:real;

A,B,C,D:real;

begin

c0:=0;

E:=0.000001;

Ymax:=1;

Ymin:=0;

Kt:=0.0956;

Ud:=0.01;

repeat

begin

y:=(Ymax+Ymin)/2;

Tf:= (Ln(y)+27.325)/ 0.01047; // обратная функция для z

Ub:= power( ( exp( Ln(y)) / 9.216e-5) , (2/3)); //обратн. функция для x

Uf:=Ub+Ud;

if y<=0 then

begin

c0:=1; // код ошибки

break;

end;

A:=Ln(y);

B:=A/(-Kt);

C:=B+z*Ud;

D:=z-Tf;

if D=0 then

begin

c0:=2; // код ошибки

break;

end;

X0:=(C/D)+Ub; // поэтапное вычисление х ( или Ua )

if X0 > x then Ymax:=y else Ymin:=y;

end until (X0+E > x) and (X0-E < x);

end;

На рисунке 5.22., где три графика построены по старому алгоритму Midi2_012, построим график по новому алгоритму для температуры 2420 K.

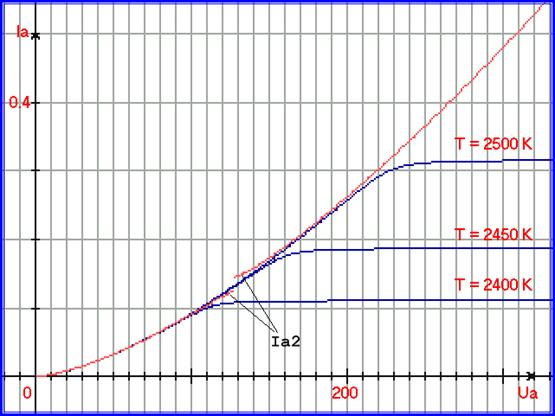
Рис. 5.22. График, иллюстрирующий двухмерный процессовый переход. Для процессов

Ia=A=F1(Ua) = 9,215∙10^-5 ∙ Ua ^3/2, и Ia = B=F2(T) = exp( 1,047∙10^-2∙T - 27,325 ), построена функция __ __

Ia _рез = Ia = exp ( -K_T∙( ( T - F2(T) )∙(Ua - F1(Ua) ) - T∙U_D ) ) , с аргументом Ua при 3-х температурах. Ось абсцисс в Вольтах, ось ординат в Амперах. По новому алгоритму, для температуры 2420 K построен график Ia2.

Заданное неверное значение для Ymax приводит к тому, что нижняя часть графика частично строиться по условию минимизации, а затем график в точке 130 Вольт перепрыгивает выше и строиться по условиям максимизации.

Это говорит о том, что алгоритм следует продумывать, и что он может приводить к ошибкам. К тому же у «эмиссионного уравнения» есть замечательное свойство - оно имеет решения и по условиям минимизации и по условиям максимизации. Это похоже на две ветви гиперболы.

Есть способ увидеть две эти ветви. На рисунке 5.23. они приведены для температуры 2420 Кельвин.

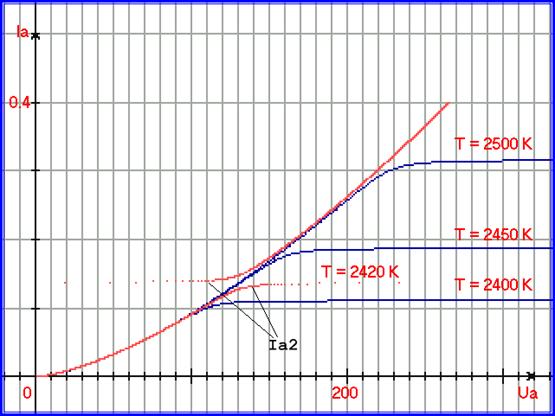
Рис. 5.23. График, иллюстрирующий двухмерный процессовый переход. Для процессов

Ia=A = F1(Ua) = 9,215∙10^-5 ∙ Ua ^3/2, и Ia = B=F2(T) = exp( 1,047∙10^-2 ∙ T - 27,325 ), построена функция __ __

Ia _рез = Ia = exp ( -K_T ∙ ( ( T - F2(T) ) ∙ (Ua - F1(Ua) ) - T∙ U_D ) ) ,