Как работает математическая модель закона Ричардсона- Дэшмана.

Температура T_F определяет некоторую температуру насыщения.

При T_F = T наступает явление насыщения. (T – температура катода.) И предельный ток, называемый «током насыщения» , вычисляется по формуле (см. (3.3.5.,01)) :

(3.3.6.,01)

Отсюда следует:

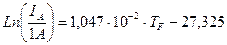(3.3.6.,02)

Это выражение может быть приведено к виду выражения (3.3.1.,10):

(3.3.6.,03)

далее:

(3.3.6.,04)

Мы привели выражение (3.3.6.,01) к эмиссионному уравнению, имеющего вид уравнения (3.3.1.,10).

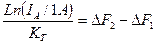(3.3.1.,10)

где

ΔF₂=0,109 ∙ (T_F-2609,8);

0.109 В - некоторое напряжение;

2609,8К – температура;

ΔF₁=0;

K_T= 0,0956 Вольт^-1 ∙ Кельвин^-1 – коэффициент;

T_F – температура (тепловое напряжение) электронов в вакууме;

I_A – ток анода.

При T_F = T ток I_A представляет собой ток насыщения I_AN . Мы получили уравнение, которое заменяет уравнение Ричардсона-Дэшмана и само является эмиссионным уравнением. Рассмотрим, почему уравнение Ричардсона – Дэшмана предоставляет нам другую математическую модель. Привожу это уравнение, как оно выглядит в одной из лабораторных работ:

(3.3.6.,05)

Здесь T – температура катода.

Узнаём, что A для вольфрама = 4,52 эВ

Зная, что J – плотность тока насыщения, переведём её в ток насыщения, умножив на коэффициент K_S.

(3.3.6.,06)

Переведём к логарифмическому виду:

(3.3.6.,07)

Отсюда мы видим, что Ln(K_S) + Ln(B) представляет собой некоторую постоянную и её всегда можно вычислить. Оставшаяся часть без постоянной, имеет вид:

(3.3.6.,08)

y = Ln( T² ) - A/(k ∙ T) (3.3.6.,09)

Постоянная Больцмана в электроновольтах имеет вид:

k = 8,617343·10^-5 эВ·К^-1 ;

Перепишем уравнение в более простой форме:

Отношение H = A/k = 4,52 / 8,617343·10^-5 = 5,245236·10⁴

(3.3.6.,10)

С – некоторая постоянная.

Уравнение Ричардсона-Дэшмана должно моделировать прямую A-A (см. рис. 1.3.) на графике в полулогарифмическом масштабе.

При С = 4,1 уравнение Ричардсона-Дэшмана пытается моделировать прямую линию. Видно, что при малых токах происходит несовпадение с экспериментальными данными эксперимента Дэшмана. (см. рис. 3.14.)

В чём я вижу несоответствие закона Ричардсона-Дэшмана опыту:

Во-первых, уравнение Ричардсона-Дэшмана было выведено из статистического уравнения распределения электронов по энергиям. И там температура была в знаменателе! Здесь привожу реальный вид уравнения:

(3.3.6.,11)

Так и следует его писать. То есть здесь распределение электронов по энергиям ничего общего не имеет с распределением Максвелла. Начинали выводить согласно статистическому распределению Максвелла, а в результате получили уравнение (3.3.6.,11) , что соответствует совсем другому статистическому распределению.

Во-вторых, уравнение Ричардсона-Дэшмана пытается моделировать прямую линию и весьма неудачно. Когда, просто проведенная прямая совпадает с большим количеством точек .

На рисунке 3.13. представлены экспериментальные данные в полулогарифмическом масштабе.

Рис. 3.13. Кривая А-А’ из эксперимента С. Дэшмана, в полулогарифмическом масштабе имеет вид прямой линии.

На рисунке 3.14. построена мат. модель для экспериментальных данных (для эксперимента С. Дэшмана) через уравнение Ричардсона-Дэшмана:

(3.3.6.,10)

при С = 4,1

Рис. 3.14. Кривая А-А’ из эксперимента С. Дэшмана, в полулогарифмическом масштабе имеет вид прямой линии. Поверх неё построена математическая модель согласно закону Ричардсона-Дэшмана :

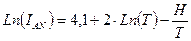
Сравните, как на рисунке 3.15. экспериментальные данные моделируются с помощью прямой линии:

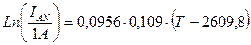(3.3.6.,12)

I_AN – ток насыщения.

Рис. 3.15. Кривая А-А’ из эксперимента С. Дэшмана, в полулогарифмическом масштабе имеет вид прямой линии. Поверх неё построена математическая модель в виде прямой :

В отличие, от уравнения Шокли, уравнение Ричардсона – Дэшмана описывает не семейство характеристик при изменении температуры, а всего одну прямую для определенного катода (и возможно для анода – ведь есть же в эмиссионном уравнении температурный напор). Уравнение Ричардсона-Дэшмана нуждается в экспериментальной проверке. Закон Ричардсона-Дэшмана заменяет собой некоторое явление природы, создаёт псевдо-физический смысл явлению термоэлектронной эмиссии, представленными в уравнении константами и размерностями.

Я предлагаю более простую альтернативную математическую модель для эксперимента Дэшмана (и соответственно модель для тока насыщения вакуумного диода):

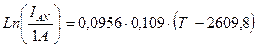(3.3.6.,03)

0,109 Вольт - некоторое напряжение.

2609,8 Кельвин – температура.

0,095 Вольт^-1 ∙ Кельвин^-1– коэффициент.

T – температура катода.

I_AN – ток насыщения анода.

В случае, если рассматривается эмиссионное уравнение ( задаётся условие: I_A = I_AN), то выражение для тока анода имеет следующий вид:

(3.3.6.,13)

Закон Ричардсона – Дэшмана для вольфрамового катода создаёт математическую модель для тока насыщения. Уравнение Шокли, в отличие от уравнения Ричардсона – Дэшмана является ложной математической моделью, так как, не проходит экспериментальную проверку. Общее для этих двух моделей – это то, что в их формулах присутствует экспонента. Экспоненты в формулах Шокли и закона Ричардсона – Дэшмана возникают в уравнениях из-за действия закона для электрического тока в условиях СТЭ-потенциалов при протекании флуктуационного тока (или теплопередачи) - см. выражение (3.3.1.,10).

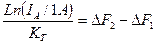(3.3.1.,10)

Выражение (3.3.1.,10) выводится из теории зарядов-энергий (3.3.2.,19) :

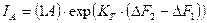(3.3.2.,19)