Расчёт вольт-амперной характеристики прямого тока для полупроводникового диода.

Нарисуем эквивалентную схему цепи прямого тока полупроводнико-вого диода.

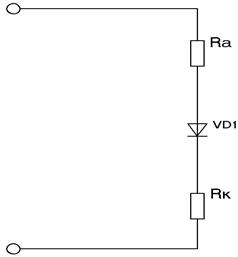
Рис. 3.17. Эквивалентная схема цепи прямого тока полупроводникового диода.

VD1 – идеальный диод, то есть диод, выводы которого не имеют омического сопротивления.

Сопротивления выводов на рисунке 3.17. отмечены отдельно как Rk и Ra. На резисторах Ra и Rk падает напряжение, что ослабляет СТЭ - потенциал. На рисунке 1.13. отметим падения напряжения.

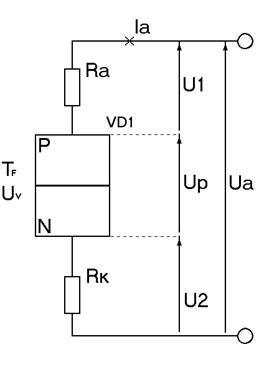
Рис. 3.18. Падения напряжений на элементах цепи рисунка 3.17.

Вычислим падение напряжения на резисторах:

(3.3.8.,01)

(3.3.8.,02)

Вычислим падение напряжения на идеальном диоде Up:

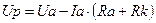(3.3.8.,03)

В зоне N, откуда движутся электроны, существует начальный составной термоэлектрический потенциал ∆F₂, который определяется температурой окружающей среды Tc и некоторой разностью потенциалов U_D.

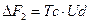(3.3.8.,04)

Второй составной термоэлектрический потенциал существует как сравнение потенциалов зоны P и зоны N. Он возникает на границе зон и имеет вид произведения потенциалов ∆U_S и ∆T_S. Выразим чему равно ∆U_S и ∆T_S:

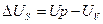(3.3.8.,05)

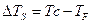(3.3.8.,06)

Из выражений (3.3.8.,05) и (3.3.8.,03) выразим ∆Us:

(3.3.8.,07)

Отсюда следует выражение для СТЭ - потенциала:

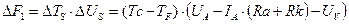(3.3.8.,08)

Теперь найдём разность СТЭ - потенциалов ∆F₂ - ∆F₁ :

(3.3.8.,09)

Согласно закона об отношении флуктуационного и электрического тока (3.3.2.,19), имеем:

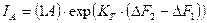(3.3.2.,19)

Далее следует:

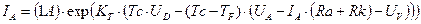(3.3.8.,10)

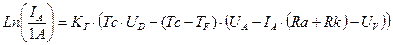(3.3.8.,11)

Получаем уравнение (3.3.8.,11), которое совпадает с эмпирическим уравнением для полупроводникового диода. В процессе моделирования, для полупроводникового диода КД213А было получено уравнение, являющиеся «эмиссионным уравнением» :

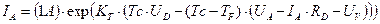(1.1.9.,05)

где:

K_T = 0,0956 Вольт^-1 ∙ Кельвин^-1;

T_F =605,2 Kельвин;

U_D = 0,276 Вольт;

Tс < T_{F ;}

Uv = 0,885 Вольт;

R_D = 0,25 Ом;

Tс – температура окружающей среды, или температура

PN-перехода (Кельвин);

U_A - напряжение на аноде;

I_A – ток анода.