Двоичная арифметика

Правила арифметических операций во всех позиционных системах одинаковы и основываются на таблицах сложения, вычитания и умножения одноразрядных чисел. В силу наибольшей распространенности двоичной системы более детально остановимся на ней.

Таблица. сложения Таблица. вычитания Таблица. Умножения

0 + 0 = 0 10 – 1 = 1 0 * 0 = 0

0 + 1 = 1 1 – 1 = 0 0 * 1 = 0

1 + 0 = 1 0 – 0 = 0 1 * 0 = 0

1 + 1 =10 1 – 0 = 1 1 * 1 = 1

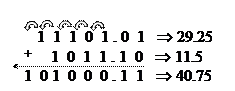Сложение двоичных чисел. Выполняется поразрядно, начиная с младшего разряда. В сложении участвуют одноименные разряды слагаемых и перенос в текущий разряд. Результатом является сумма в текущем разряде и перенос в следующий разряд. В зависимости от значения слагаемых перенос будет равен 0 (нет переноса) или 1 (есть перенос). ЭВМ имеет специальное устройство, предназначенное для сложения двоичных чисел. Это устройство называется сумматором. Сумматор реализует сложение через комбинацию логических операций. Логические операции будут рассмотрены позже.

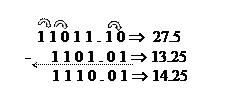Вычитание двоичных чисел. Выполняется поразрядно, начиная с младшего. При необходимости выполняется заем двойки из соседнего старшего разряда. ЭВМ обычно не имеет специального вычитающего устройства. За счет применения специальных кодов операция вычитания заменяется на операцию сложения.

Умножение двоичных чисел. Выполняется путем последовательного умножения цифр множителя на множимое и сложение частичных сумм. Количество цифр в дробной части результата равно суммарному количеству цифр в дробных частях сомножителей. Пример умножения приведен на Рис.1. В ЭВМ умножение реализуется путем сдвига множимого и прибавление его к сумме, если цифра множителя равна единице.

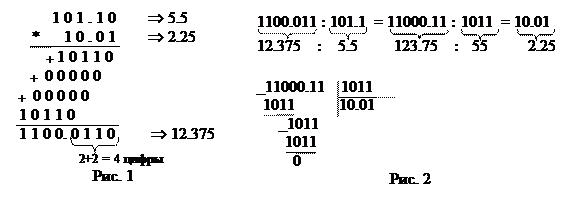Деление двоичных чисел. Реализуется путем последовательных умножений цифр результата на делитель и вычитания из делимого. Пример деления приведен на Рис.2.

При выполнении операций сложения и вычитания вручную удобнее пользоваться восьмеричной или шестнадцатеричной системой. Рассмотрим особенности выполнения операций в этих системах счисления.

Если при сложении одноименных разрядов и переноса получено число N<S, то оно берется в качестве суммы разряда, а перенос в следующий разряд равен 0. Если получено число N³S, то в качестве суммы берется разность N-S и формируется единица переноса в следующий разряд. При сложении нескольких чисел сумма одноименных разрядов может превысить основание системы счисления в несколько раз. В этом случае необходимо пользоваться общим правилом: в качестве суммы берется остаток от целочисленного деления N/S, а значение переноса в следующий разряд есть целая часть от деления N/S.

При вычитании разрядов при необходимости берется заем из старшего разряда. Вычитание производится из суммы S+A_i, где A_i – значение i-го разряда вычитаемого. Значение разряда, из которого производился заем, уменьшается на 1.

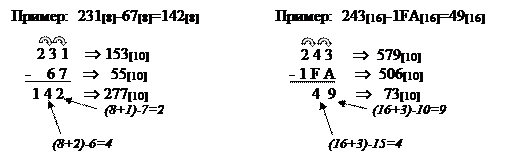Операции умножения и деления в этих системах менее удобны для ручного выполнения, так как требуют знания таблиц умножения для восьмеричных или шестнадцатеричных чисел.