Способы описания логических функций

Применяются три основных способа описания логических функций: аналитический, табличный и графический.

При аналитическом способе функция записываются в виде логического выражения.

При табличном способе функция записывается в виде таблицы истинности. Число строк в таблице истинности равно числу комбинаций переменных, т.е 2ⁿ, где n - число логических переменных. Таблицу истинности можно составить по аналитической записи путем подстановки всех комбинаций значений переменных.

Преобразование таблицы истинности в аналитическую запись выполняется по методу совершенной дизъюнктивной нормальной формы (СДНФ) или методу совершенной конъюнктивной нормальной формы (СКНФ).

СДНФ–функция, образованная сложением всех конституант единицы. Конституанта единицы составляется для тех комбинаций переменных, на которых функция равна единице. Конституанта единицы – это логическое умножение всех переменных, причем переменные, имеющие значение 0, берутся с инверсией. Составим аналитическую запись логической функции двух переменных по заданной таблице истинности.

Номер комбинации	x1	x2	Y

В рассматриваемом примере логических переменных две, т.о. количество комбинаций 2²=4. Комбинациям в строчках 2 и 3 соответствует единичное значение функции. Именно для них составляются конституанты 1.В результате сложения конституант 1 получим аналитическую запись функции по методу СДНФ:

Y = `x<sub>1</sub> · x<sub>2</sub> + x<sub>1</sub> ·`x₂

Метод СДНФ целесообразно применять, когда в таблице истинности преобладают нулевые значения функции.

СКНФ –функция, образованная умножением всех конституант нуля. Конституанта нуля составляется для тех комбинаций переменных, на которых значение логической функции равно нулю. Конституанта нуля – это логическое сложение всех переменных, причем переменные, имеющие значение 1, берутся с инверсией. Составим аналитическую запись логической функции по таблице истинности, рассмотренной в предыдущем примере. Комбинациям в строчках 1 и 4 соответствует нулевое значение функции. Именно для них составляются конституанты 0. Путем умножения конституант 0 получим СКНФ:

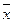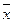Y = (x₁ + x₂ ) · ( ₁ + ₂)

Метод СКНФ целесообразно применять, когда в таблице истинности преобладают единичные значения функции.

Логические функции считаются тождественными, если их значения совпадают при всех комбинациях аргументов. Т.о. тождественность логических функций может быть проверена путем сопоставления их таблиц истинности.

Альтернативным путем проверки логических функций на тождественность является преобразование логических функций до совпадения их аналитической записи. Проверим тождественность полученных выше логических функций аналитическим путем.

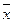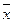Y= (x₁ + x₂ )( ₁ + ₂) = =

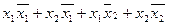Имеем совпадение аналитической записи обеих логических функций, следовательно, они тождественны.