Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Эти преобразования наиболее просты, так как восьмеричные и шестнадцатеричные числа представляют собой не что иное, как компактную форму записи двоичных чисел. Преобразование базируются на том, что основание одной системы является степью двойки основания другой системы:

2³ = 8, поэтому восьмеричную цифру можно представить группой из трех двоичных цифр. Группа из трех двоичных цифр называется триадой;

2⁴ = 16, поэтому шестнадцатеричную цифру можно представить группой из четырех двоичных цифр. Группа из четырех двоичных цифр называется тетрадой.

Преобразование «2 ® 8».Двигаясь от точки влево и вправо разбить цифры исходного двоичного числа на триады. При необходимости дополнить число слева и справа не значащими нулями. Каждую триаду заменить восьмеричной цифрой.

На рисунке приведен пример преобразования двоичного числа 1011110.10111 в восьмеричное число 136.56. Для образования триад слева добавлены два нуля, а справа один.

Преобразование «2 ® 16».Правила аналогичны преобразованию «2 ® 8», но исходное двоичное число разбивается на тетрады.

На рисунке приведен пример преобразования двоичного числа 110111110.001111 в шестнадцатеричное число 1BE.3C. Для образования тетрад слева добавлены три нуля, а справа два.

Преобразование «8 ® 2».Это преобразование противоположно преобразованию «2 ® 8». Каждая цифра исходного восьмеричного числа заменяется триадой, содержащей двоичный эквивалент восьмеричной цифры. Незначащие левые и правые нули можно отбросить.

На рисунке приведен пример преобразования восьмеричного числа 203.4 в двоичное число 10000011.1. Слева отброшен один незначащий ноль, а справа - два незначащих нуля.

Преобразование «16 ® 2».Это преобразование противоположно «2 ® 16». Каждая цифра исходного шестнадцатеричного числа заменяется тетрадой, содержащей двоичный эквивалент шестнадцатеричной цифры. Незначащие левые и правые нули можно отбросить.

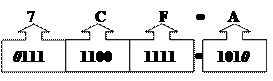На рисунке приведен пример преобразования шестнадцатеричного числа 7CF.A в двоичное число 11111001111.101. Слева и справа отброшено по одному незначащему нулю.

Дляполучения двоичной тетрады, эквивалентной восьмеричной цифре, можно использовать правило “421”, в основе которого лежит представление числа в виде суммы степеней двойки. В триаде необходимо записать единицы на местах цифр, сумма которых дает значение восьмеричной цифры. На местах остальных цифр записать ноль.

Примеры:7_[8] = 4 + 2 +1 Þ 111_[2]

3_[8] = 2 +1 Þ 011_[2]

6_[8] = 4 + 2 Þ 110_[2]

5_[8] = 4 + 1 Þ 101_[2]

Для получения двоичной тетрады, эквивалентной шестнадцатеричной цифре, можно использовать правило “8421”. В тетраде необходимо записать единицы на местах цифр, сумма которых дает значение шестнадцатеричной цифры. На местах остальных цифр записать ноль

Примеры:F_[16] = 15_{[10] =} 8 + 4 + 2 + 1 Þ 1111_[2]

C_[16] = 12_{[10] =} 8 + 4 Þ 1100_[2]

D_[16] = 13_{[10] =} 8 + 4 + 1 Þ 1101_[2]

9_[16] = 9_{[10] =} 8 + 1 Þ 1001_[2]