МАТЕМАТИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ
Основным средством реализации информационных процессов являются электронно-вычислительные машины (ЭВМ). ЭВМ представляет собой техническое устройство, предназначенное для автоматического выполнения алгоритма. Современные ЭВМ способны обрабатывать информацию различных видов: числовую, текстовую, звуковую, изображения и т.д. Информация любого вида в конечном итоге преобразуется к числовой форме. Это преобразование называют оцифровкой данных. Представление чисел и их обработка в ЭВМ составляет основу информационных процессов.
Системы счисления
Система счисления – совокупность символов и правил для наименования и обозначения чисел. Символы называются цифрами. Классификация систем счисления в зависимости от способа определения числового эквивалента цифр приведена на рисунке.
 Позиционные системы счисления имеют более простые правила выполнения арифметических операций, что обусловило их повсеместное использование. При обработке данных в ЭВМ в основном используются двоичная, восьмеричная, шестнадцатеричная и десятичная позиционные системы счисления.
Позиционные системы счисления имеют более простые правила выполнения арифметических операций, что обусловило их повсеместное использование. При обработке данных в ЭВМ в основном используются двоичная, восьмеричная, шестнадцатеричная и десятичная позиционные системы счисления.
Аппаратные средства ЭВМ рассчитаны на представление и обработку двоичных данных. Объясняется это простотой реализации электронного устройства, имеющего два устойчивых состояния. Одно из состояний принимается за 0, другое за 1. За простоту реализации приходится платить большим количеством цифр в записи числа. Двоичное число в среднем в 3,3 раза длиннее десятичного.
Восьмеричная и шестнадцатеричная системы широко используется для записи двоичных чисел в компактной форме. Такая форма применяется в технической документации для ЭВМ и в программах на машинно-ориентированных языках.
Для записи данных в программах на языках высокого уровня используется, в основном, привычная для человека десятичная система счисления. Преобразование к двоичному виду выполняется при переводе программы на машинный язык.
В общем виде число в позиционной системе счисления записывается в виде полинома:
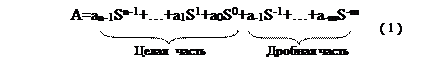 |
где S – основание системы, ai – одна из цифр алфавита этой системы счисления.
При сокращенной записи числа основание системы счисления подразумевается, а цифры целой и дробной части разделяются точкой:
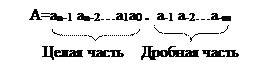
Каждая цифра в записи числа называется разрядом. Для двоичных чисел вместо термина разряд часто используют термин бит. Каждый левый разряд имеет вес в S раз больший, чем предыдущий. Крайний правый разряд имеет наименьший вес и называется младшим разрядом. Крайний левый разряд имеет наибольший вес и называется старшим разрядом.
Пусть на запись числа отведено n+m разрядов, из них n на целую часть и m на дробную часть. Число рассматривается как число без знака. Определим максимальное и минимальное число, которое может быть записано в этой разрядной сетке:
| n=3 | m=2 | ||||||
| . | |||||||
 Максимальное число Amax = (Sn – 1) + (1 - S-m)
Максимальное число Amax = (Sn – 1) + (1 - S-m)


Например, для десятичной системы при n=3 и m=2 максимальное число
Amax = (103–1) + (1-10-2) = (1000-1) + (1–0.01) = 999 + 0.99 = 999.99
Для получения записи максимального числа необходимо занести во все разряды наибольшую цифру системы счисления.
| n=3 | m=2 | ||||||
| . | |||||||
Минимальное отличное от нуля число Amin= 0 + S-m



Например, для десятичной системы при n=3 и m=2 минимальное число
Amin = 10-2 = 0.01
Для получения записи минимального числа необходимо занести в младший разряд единицу, а в остальные разряды нули.
Количество различных комбинаций цифр Nк определяет количество различных по значению чисел, которые могут быть записаны в заданных разрядах:
Nк = Sm+n
Для рассмотренного примера количество десятичных чисел Nк=105
При работе с технической документацией и анализе машинных программ приходится выполнять преобразования чисел из одной системы счисления в другую. Общие правила преобразования будут рассмотрены ниже.
В таблице приведена запись первых 20-ти чисел в разных системах счисления:
| A10 | A2 | A8 | A16 | A10 | A2 | A8 | A16 | |
| A | ||||||||
| B | ||||||||
| C | ||||||||
| D | ||||||||
| E | ||||||||
| F | ||||||||
Дата добавления: 2019-02-08; просмотров: 1356;











