Графическое описание логической функции
Графическое представление чаще всего применяется для описания схемы устройства, которое реализует заданную функцию. Логические функции в этом случае называют переключательными функциями. Рассмотрим основные переключательные функции и их условные графические обозначения.








 Y =`x (НЕ) x1Y x &Y Функция инверсии.
Y =`x (НЕ) x1Y x &Y Функция инверсии.
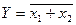 (ИЛИ-НЕ)
(ИЛИ-НЕ)

 x1 1 Y Функцию ИЛИ-НЕ иногда называют стрелкой Пирса.
x1 1 Y Функцию ИЛИ-НЕ иногда называют стрелкой Пирса.


 x2 Функция определена для любого числа аргументов.
x2 Функция определена для любого числа аргументов.
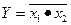 (И-НЕ)
(И-НЕ)

 x1 & Y Функцию И-НЕ иногда называют стрелкой Пирса.
x1 & Y Функцию И-НЕ иногда называют стрелкой Пирса.


 x2 Функция определена для любого числа аргументов.
x2 Функция определена для любого числа аргументов.
Набор функций, из которого методом суперпозиции можно получить любую переключательную функцию, называется логически (функционально) полным. Функционально полный набор образуют логическое сложение, умножение и инверсия. Причем сложение по закону де Моргана можно заменить умножением с инверсией аргументов. Аналогично умножение можно заменить сложением с инверсией аргументов. Таким образом, каждая из функций ИЛИ-НЕ и И-НЕ является функционально полной.
В ЭВМ широко используются функции двух переменных для проверки их равнозначности или неравнозначности.Формально они не относятся к основным, так как их можно реализовать на базе рассмотренных выше функций. Но ввиду распространенности на практике эти функции часто относят к основным функциям. Рассмотрим условные обозначения и логику этих функций.
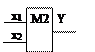 Y = x1Åx2 =
Y = x1Åx2 =  (М2). Функция неравнозначности. Используется для арифметического сложения аргументов по модулю 2 и проверки переменных на несовпадение их значений.
(М2). Функция неравнозначности. Используется для арифметического сложения аргументов по модулю 2 и проверки переменных на несовпадение их значений.

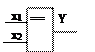
Y = x1Åx2 (= =). Функция равнозначности. Используется для проверки переменных на совпадения их значений. Эта функция представляет собой инверсию функции неравнозначности.
Таблица истинности функции Таблица истинности функции
неравнозначности (М2) равнозначности 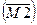
| x1 | x2 | Y | x1 | x2 | Y | ||||||
Дата добавления: 2019-02-08; просмотров: 929;











