Двоичная система счисления
Арифметические основы вычислительной техники
Системы счисления
В ЭВМ информация всегда представляется в виде чисел, записанных в той или иной системе счисления. Выбор системы счисления - один из важнейших вопросов. От правильности его решения зависят такие характеристики ЭВМ, как скорость вычислений, сложность алгоритмов реализации арифметических операций и др. Система счисления - совокупность цифр, приемов и правил для записи чисел цифровыми знаками.
Любая система счисления должна обеспечивать:
§ возможность представления любого числа в рассматриваемом диапазоне величин;
§ единственность этого представления;
§ простоту оперирования числами.
Различают два типа систем счисления - непозиционные и позиционные.
Непозиционная система счисления - система, для которой значение символа не зависит от его положения в числе. Примером может служить система счисления с одной цифрой 1. Для записи любого числа в ней необходимо написать количество единиц, равное числу. Другой пример - это римская система счисления.
Позиционной системой счисления называется система записи любых по величине чисел, в которой значение цифры зависит от ее положения в числе, т.е. веса. Число цифр в позиционной системе счисления ограниченно.
Основание (базис) r позиционной системы счисления - максимальное количество различных знаков или символов, используемых для изображения числа в данной системе счисления. Таким образом, основание может быть любым числом, кроме 1 и бесконечности.
Любое число в системе счисления с основанием r может быть записано в общем виде:
A=an·rn+ an-1·rn-1+...+a1·r1+a0·r0+ a-1·r--1+...+a-rn-1·r-(rn-1)+a-rn·r-rn, (1)
или
 , (2)
, (2)
где любая разрядная цифра aiÎ{0,…,r-1}, a ri - вес соответствующего разряда.
Запись числа в форме (1) назовем записью числа в развернутой форме. Свернутой формой записи чисел называется запись чисел в виде
A=a1a2 … ak.
Для любой системы счисления основание представляется как 1 (один) и 0 (ноль).
Например: 9 1 F 7
+1 +1 +1 +1
1010 102 1016 108
Вес разряда pi числа выражается соотношением
pi = ri /r0 = ri ,
где i - номер разряда при отсчете справа налево.
Если в i-м разряде накопилось значение единиц, равное или большее r, то должна происходить передача единицы в старший i+1 разряд. При сложении такая передача информации называется переносом. При вычитании передача из i+1 разряда в i-й – заем.
Длина числа – количество позиций (разрядов) в записи числа. В технической реализации под длиной числа понимается длина разрядной сетки.
Диапазон представления чисел в заданной системе счисления – интервал числовой оси, заключенный между максимальным и минимальным числами, представленными при заданной длине разрядной сетки.
В вычислительной технике для представления данных и выполнения арифметических операций над ними удобно использовать двоичную, восьмеричную и шестнадцатеричную системы счисления. Ниже коротко остановимся на них.
Двоичная система счисления
Для записи числа в двоичной системе счисления используются две цифры: 0 и 1. Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью высоких и низких потенциалов или группой запоминающих элементов, способных запоминать одно из двух (0,1) значений. Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной системе счисления.
| Сложение | Вычитание | Умножение | ||||
| 0+0= 0 | 0-0=0 | 0 · 0=0 | ||||
| 0+1= 1 | 1-0=1 | 0 · 1=0 | ||||
| 1+0= 1 | 1-1=0 | 1 · 0=0 | ||||
| 1+1=10 | 10-1=1 | 1 · 1=1 |
Рассмотрим несколько примеров, демонстрирующих выполнение арифметических операций:
|
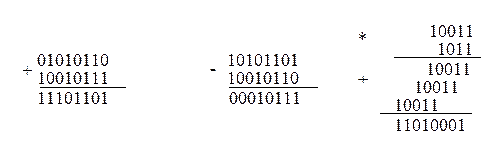
Дата добавления: 2022-02-05; просмотров: 450;











