Преобразования из десятичной системы счисления в любую другую систему
Преобразование выполняется отдельно для целой и дробной части числа. Все операции выполняются по правилам десятичной арифметики. Основание новой системы рассматривается как десятичное число.
Преобразование целой части выполняется путем последовательного деления целой части на основание новой системы. На каждом шаге вычисляется целая часть и остаток от деления. Остатки и есть значение цифр числа в новой системе счисления. Полученные остатки записываются в новой системе счисления. На первом шаге будет получена младшая цифра. Процесс продолжается, пока очередная целая часть не окажется меньше основания новой системы счисления. Эта целая часть есть старшая цифра числа.
Правила перевода следуют из формы записи числа в позиционной системе счисления:
 Шаг 1 A10 = an-1Sn-1+…+a1S1+ a0 | :S Þ an-1Sn-2 +…+ a1S0 +
Шаг 1 A10 = an-1Sn-1+…+a1S1+ a0 | :S Þ an-1Sn-2 +…+ a1S0 + 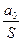 ® a0
® a0
Целая часть Остаток
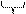 Шаг 2 A10 = an-1Sn-2+…+a2S1+ a1 | : S Þ an-1Sn-3 +…+ a2S0 +
Шаг 2 A10 = an-1Sn-2+…+a2S1+ a1 | : S Þ an-1Sn-3 +…+ a2S0 + 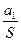 ® a1
® a1
Целая часть Остаток
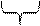 Шаг n-1 A10 = an-1S1+ an-2 | : S Þ an-1 +
Шаг n-1 A10 = an-1S1+ an-2 | : S Þ an-1 + 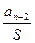 ® an-2
® an-2
Целая часть Остаток
 | 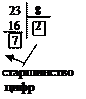 | 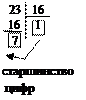 | |||
Пример: 23[10] ® ?[2] Пример: 23[10] ® ?[8]Пример: 23[10] ® ?[16]
10111[2] 27[8] 17[16]
Преобразование дробной части выполняется путем последовательного умножения дробной части на основание новой системы. На каждом шаге выделяется новая целая часть и новая дробная часть. Последовательность целых частей дает значение цифр числа в новой системе счисления. На первом шаге будет получена старшая цифра дробной части в новой системе. Процесс продолжается до получения заданного количества значащих цифр или нулевого значения дробной части.
Правила перевода следуют из формы записи числа в позиционной системе счисления:
Шаг 1 A10 = a-1S-1 + a-2S-2 +…+a-mS-m | * S Þ a-1 + a-2S-1 + … +a-mS-m+1
 | |||
 | |||
Целая часть Дробная часть
Шаг 2 A10 = a-2S-1 +…+a-mS-m+1 | * S Þ a-2 + a-3S-1 + … +a-mS-m+2
 |  | ||
Целая часть Дробная часть

 Целая часть Дробная часть
Целая часть Дробная часть
0 125 * 2

 0 250 * 2
0 250 * 2
0500 * 2
 1000
1000
 Целая часть Дробная часть
Целая часть Дробная часть
0 55 * 16

 8800 *16
8800 *16
C800 *16
C800
Дата добавления: 2019-02-08; просмотров: 879;











