Группы формул Максвелла
Рассмотрим систему из трех проводов вблизи проводящей поверхности.
Возьмем в диэлектрике некоторую произвольную точку М.
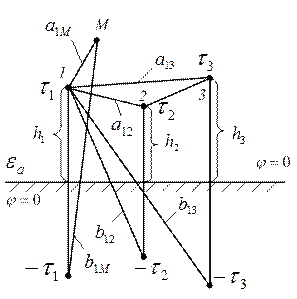
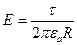 ;
;
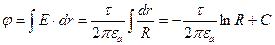 .
.
Потенциал точки М будет равен сумме потенциалов создаваемых каждым проводом и его зеркальным изображением:
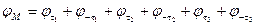 ;
;
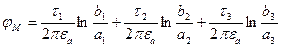 .
.
Поместим точку М на поверхность первого провода:
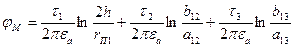 .
.
Обозначим
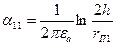 ;
; 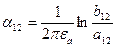 ;
; 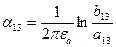 ,
,
где 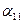 ,
, 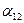 ,
, 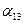 – потенциальные коэффициенты
– потенциальные коэффициенты 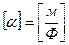 .
.
Перемещая точку М с первого на второй и третий провод, получим систему уравнений
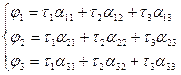 – первая группа формул Максвелла.
– первая группа формул Максвелла.
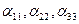 – собственные коэффициенты
– собственные коэффициенты
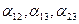 – взаимные коэффициенты
– взаимные коэффициенты
Так как 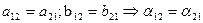 .
.
Все 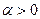 , т.к.
, т.к. 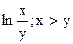 .
.
Кроме первой группы формул Максвелла есть 2 и 3 группы формул Максвелла.
Во второй группе формул Максвелла по известным потенциалам тел находят заряды тел (потенциалы), т.е. решают обратную задачу.
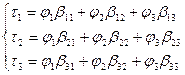 – вторая группа формул Максвелла.
– вторая группа формул Максвелла.
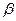 – ёмкостной коэффициент.
– ёмкостной коэффициент. 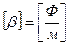 .
.
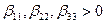 – собственные коэффициенты
– собственные коэффициенты
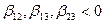 – взаимные коэффициенты
– взаимные коэффициенты
Для перехода из первой группы формул Максвелла во вторую составляем матрицу, а затем берем обратную матрицу:
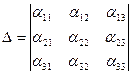
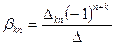 .
.
Алгебраическое дополнение получают из определителя системы путем вычеркивания К-й строки и N-го столбца и умножая на минор.
Так как определитель системы симметричен относительно главной диагонали, то
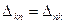 и
и 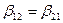 .
.
При экспериментах удобней использовать напряжение, поэтому пользуются третьей группой формул Максвелла.
В третьей группе формул Максвелла по известным потенциалам тел находят напряжение между телами:
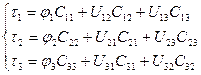 – третья группа Максвелла,
– третья группа Максвелла,
где С – частичные емкости.
С одинаковым индексом – собственные, с разноименным – взаимные.
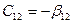 ;
;
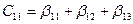 ;
;
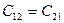 ;
;
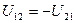 .
.
Поскольку 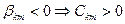 .
.
Вывод третьей группы формул Максвелла:
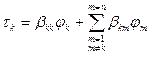 ;
;
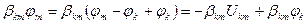 ;
;
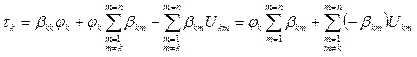 ;
;
Обозначим:
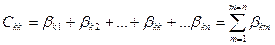 ;
;
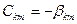 .
.
Тогда
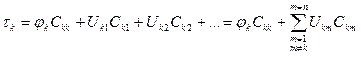 .
.
Если придать k значения 1, 2, 3, …, то получим третью группу формул Максвелла:
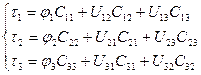
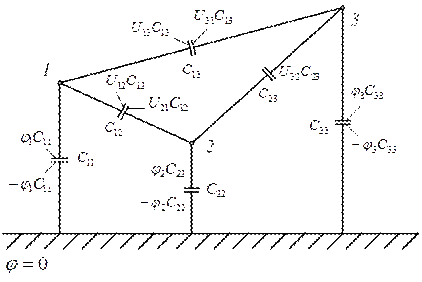
Три группы формул Максвелла справедливы для заряженных тел любой формы. Однако приведенные формулы справедливы только для параллельных, достаточно длинных проводов. Следовательно, для тел другой формы определение емкостных коэффициентов производят экспериментально (методика приведена в ТОЭ ч.3 стр 47 новое издание).
Дата добавления: 2020-10-14; просмотров: 672;











