Поляризация диэлектриков
Заряды бывают свободными и связанными.
Свободные заряды – заряды, которые под воздействием сил поля свободно перемещаются в веществе.
Связанные заряды – заряды, которые входят в состав вещества и неотделимы от него, перемещение их ограничено внутримолекулярными силами.
Под поляризацией понимают упорядоченное изменение расположения связанных зарядов в теле, вызванное электрическим полем. Отрицательные заряды в теле переместятся в сторону более высокого потенциала, а положительные в сторону более низкого потенциала.
Молекулы в электрическом отношении представляют собой диполи, которые под действием поля ориентируются таким образом, чтобы их электрический момент был направлен параллельно вектору напряженности электрического поля.
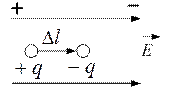
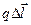 – электрический момент, направленный от “–” к “+”.
– электрический момент, направленный от “–” к “+”.
Электрический момент суммы диполей, находящихся в объеме вещества V, отнесенный к объему V, называют вектором поляризации.
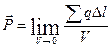 ;
; 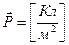 .
.
В однородных изотропных (свойства одинаковы по всем направлениям) диэлектриках вектор поляризации Р пропорционален напряженности электростатического поля.
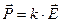 ,
,
где k – коэффициент электрической восприимчивости (определяется экспериментально).
Запишем формулу для расчета вектора электрического смещения 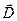 . Вектор электрического смещения
. Вектор электрического смещения 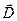 равен сумме двух векторов характеризующих поле в вакууме и поляризованности.
равен сумме двух векторов характеризующих поле в вакууме и поляризованности.
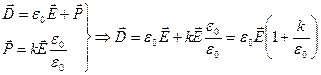 ,
,
где 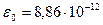 ;
;
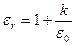 – относительная диэлектрическая проницаемость среды.
– относительная диэлектрическая проницаемость среды.
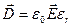 ;
;
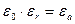 .
.
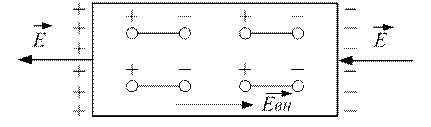
Нарисуем картину поля вокруг плоского конденсатора, внутри которого находиться диэлектрик.

Поле зарядов сориентировано навстречу внешнему полю, поэтому внутри диэлектрика поле слабее, чем внешнее поле.
Проводящее тело

В проводящем теле, по определению электростатики (заряды неподвижны) во всех точках поля потенциал одинаковый, следовательно напряженность поля равна нулю, т.е. внутри поля нет.
Поверхность тела эквипотенциальна, 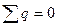 – суммарный заряд равен нулю, но так как заряды разделены, то проводящее тело влияет на внешнее поле внутри его. Если внутри проводящего тела, будет пространство, поля внутри него не будет, т.е. внешнее поле компенсируется полем зарядов, расположенных на поверхности тела. Это явление используют при электростатическом экранировании.
– суммарный заряд равен нулю, но так как заряды разделены, то проводящее тело влияет на внешнее поле внутри его. Если внутри проводящего тела, будет пространство, поля внутри него не будет, т.е. внешнее поле компенсируется полем зарядов, расположенных на поверхности тела. Это явление используют при электростатическом экранировании.
Граничные условия
В электростатическом поле рассматривают два типа границ:
1. Диэлектрик – Проводник.
2. Диэлектрик – Диэлектрик.
Для каждого типа границы есть два граничных условия:
1. Для первого типа границы Диэлектрик – Проводник:
а) отсутствует тангенциальная (касательная к поверхности) составляющая вектора напряженности электрического поля
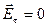 .
.
б) вектор электрического смещения D в любой точке диэлектрика, непосредственно примыкающей к поверхности тела, численно равен плотности заряда на поверхности проводящего тела в этой точке
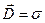
Докажем это:
а) Так как тело проводящее  , то
, то 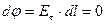 .
.
Так как 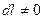 , то
, то 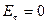 .
.
б) Мысленно выделим бесконечно малый параллелепипед. Верхняя грань расположена на поверхности проводящего тела, нижняя в диэлектрике. Параллелепипед малой толщины (сплющенный). Применим к нему теорему Гаусса в интегральной форме
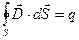 .
.
Пренебрегаем потоком через боковые грани, так как параллелепипед плоский. Поток через «дно» отсутствует, так внутри проводящего тела 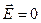 и
и 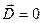 . Есть поток только через верхнею грань
. Есть поток только через верхнею грань 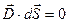 .
.
Тогда теорема Гаусса запишется:
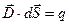 .
.
Так как угол между вектором 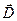 и вектором нормали
и вектором нормали 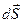 равен нулю, то:
равен нулю, то:
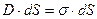 ;
;
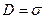 .
.
2. Для второго типа границы Диэлектрик – Диэлектрик:
а) тангенциальные составляющие поля равны
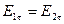 .
.
б) равны нормальные составляющие электрического смещения
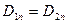 .
.


Докажем это:
а) Выделим плоский замкнутый контур mnpqm и составим вдоль него циркуляцию вектора напряженности электрического поля. Составляющими интеграла 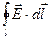 вдоль вертикальных сторон в силу их малости пренебрежем.
вдоль вертикальных сторон в силу их малости пренебрежем.
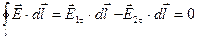 ;
;
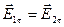 .
.
б) Мысленно выделим на границе раздела двух сред бесконечно малый параллелепипед. Внутри выделенного объема нет свободных зарядов, поэтому
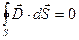 .
.
Поток вектора 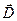 через верхнею грань:
через верхнею грань:
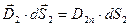 .
.
Поток вектора 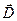 через нижнюю грань:
через нижнюю грань:
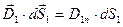 ;
;
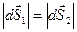 ;
;
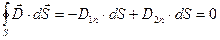 ;
;
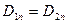 .
.
Если вектор электрического смещения 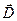 подходит под 90 градусов к границе раздела, то
подходит под 90 градусов к границе раздела, то 
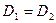
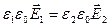 ;
;
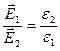 .
.
Граничные условия необходимо учитывать для любой задачи расчета поля вблизи 2–х сред. На их базе разработан ряд методов для расчета полей в пограничной зоне.
Дата добавления: 2020-10-14; просмотров: 611;











