Основные уравнения и законы
Закон Ома в дифференциальной форме
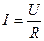 - закон Ома в интегральной форме.
- закон Ома в интегральной форме.
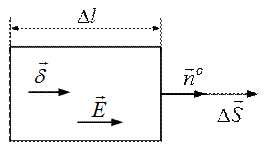
Выделим в проводящей среде небольшой объем (трубку), где 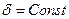 .
.
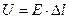
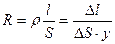
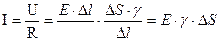
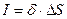 - по определению плотности тока
- по определению плотности тока
Приравняем правые части уравнений:
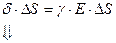
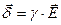 - дифференциальная форма (случай если точка находится в проводящей среде).
- дифференциальная форма (случай если точка находится в проводящей среде).
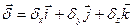
Закон Ома в дифференциальной форме устанавливает связь между плотностью тока в данной точке проводящей среды и напряженностью поля в этой точке. Уравнение справедливо для областей вне источников ЭДС, у которых удельная проводимость постоянна по всему объему.
В областях, занятых источниками ЭДС, кроме электростатического поля существует стороннее поле, обеспечивающее непрерывное движение зарядов в электрической сети. Сторонние источники э.д.с. – устройства, преобразующие энергию (механическую или другой тип энергии) в электроэнергию.
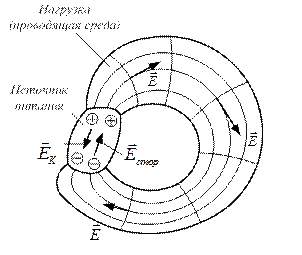
Под действием сторонней э.д.с. в источнике происходит постоянное разделение электрических зарядов. Положительные к «+» полюсу, отрицательные - к «-» полюсу, эти заряды внутри и вне источника создают эклектическое поле, напряженность которого направлена от положительных зарядов к отрицательным. Внутри источника поле сосредоточенных зарядов (кулоново поле) направленно навстречу стороннему.
Если точка находится внутри источника, то полное значение напряженности поля: 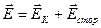
тогда 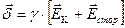
Это уравнение называют обобщенным законом Ома в дифференциальной форме или вторым законом Кирхгофа в дифференциальной форме.
Первый закон Кирхгофа в дифференциальной форме
Сумма тока, входящего в объем. равна сумме токов, из него выходящих.
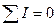
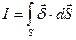 - в интегральной форме,
- в интегральной форме,
тогда из первого закона Кирхгофа 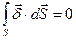
Разделим правую и левую части на объем V:
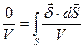
Устремим объем к нулю:

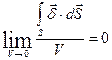
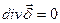
Первое уравнение Кирхгофа в дифференциальной форме – это уравнение непрерывности линий плотности тока. Оно означает, что в установившемся режиме в любой точке поля нет ни стока, ни истока линий плотности тока, линии плотности замкнуты сами на себя (окружности, эллипсы).
Дифференциальная форма закона Джоуля- Ленца
В проводнике выделяется энергия
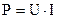
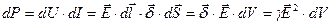
Определим энергию, выделяющуюся в единице объема в единицу времени в проводящем теле:
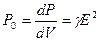
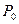 - мощность тепловых потерь
- мощность тепловых потерь
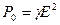 - дифференциальная форма закона Джоуля - Ленца
- дифференциальная форма закона Джоуля - Ленца
Уравнение Лапласа для электрического поля постоянного тока
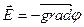
Это выражение справедливо и для электрического поля постоянного тока

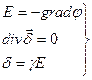
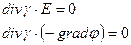
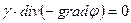
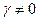
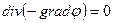
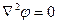 - уравнение Лапласа.
- уравнение Лапласа.
Граничные условия
При рассмотрении поля с различными проводимостями используют два граничных условия:
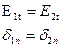
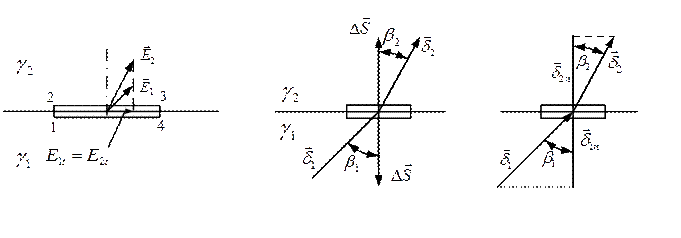
Рассмотрим первое граничное условие 
Выделим плоский замкнутый контур 1234 на границе раздела двух сред и составим вдоль него циркуляцию вектора напряженности электрического поля. Составляющими интеграла 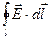 вдоль сторон 12 и 34 в силу их малости пренебрежем.
вдоль сторон 12 и 34 в силу их малости пренебрежем.
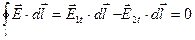
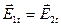
Рассмотрим второе граничное условие 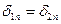
Мысленно выделим на границе раздела двух сред бесконечно малый параллелепипед. Из первого закона Кирхгофа 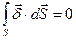
Поток вектора 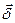 через верхнюю грань
через верхнюю грань
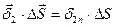
Поток вектора 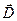 через нижнюю грань
через нижнюю грань
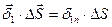
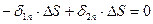
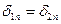
Полные значения вектора напряженности электрического поля постоянного тока и плотности тока в общем случае на границе раздела меняются скачком.
Найдем связь между углом падения 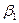 и преломления
и преломления 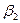
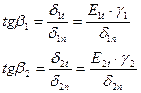
Рассмотрим частный случай, когда проводимость второй среды стремится к нулю
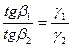 ;
; 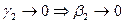
Дата добавления: 2020-10-14; просмотров: 721;











