Расчет на границе раздела двух сред
Поле заряженной оси, расположенной вблизи проводящей плоскости
(Диэлектрик - Проводник)
Заряженная ось расположена в диэлектрике параллельно поверхности проводящей среды. Требуется определить характер поля в верхней полуплоскости (диэлектрике).
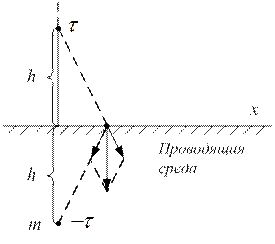
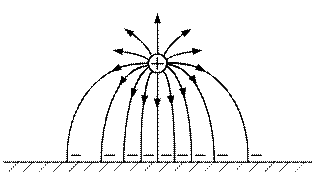
В результате электростатической индукции на поверхности проводящего тела выступают заряды. Плотность их меняется с изменением координаты x. Эти заряды влияют на поле и их влияние надо учитывать. Учесть влияние зарядов, выступивших на поверхности проводящего тела вследствие электростатической индукции, очень сложно, так как надо знать закон распределения их по поверхности проводящего тела. Данную задачу легко можно решить, используя метод зеркальных изображений. Согласно методу влияние зарядов, расположенных на поверхности проводящего тела, учитывается введением фиктивного сосредоточенного заряда, расположенного в зеркальном отражении относительно границы, при этом считается, что все пространство заполнено диэлектриком. Фиктивный заряд равен по модулю действительному и имеет противоположный знак.
Докажем это. Напряженность поля от двух зарядов 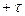 и
и 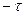 в любой точке поля имеет только нормальную к границе составляющую (выполнено граничное условие
в любой точке поля имеет только нормальную к границе составляющую (выполнено граничное условие 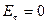 ). Потенциал от каждой из осей удовлетворяет уравнению Лапласа
). Потенциал от каждой из осей удовлетворяет уравнению Лапласа 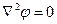 (вывод уч. Бессонов ТОЭ стр. 42 (формула для потенциала заряженной оси подставляется в уравнение Лапласа в цилиндрической системе координат)). На основании теоремы единственности решения полученное решение является истинным.
(вывод уч. Бессонов ТОЭ стр. 42 (формула для потенциала заряженной оси подставляется в уравнение Лапласа в цилиндрической системе координат)). На основании теоремы единственности решения полученное решение является истинным.
Пример:
Заряженная ось, расположена в диэлектрике параллельно поверхности проводящей среды. Требуется определить напряженность электростатического поля и потенциал в точке А.
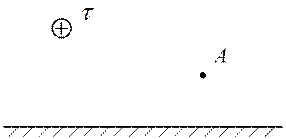
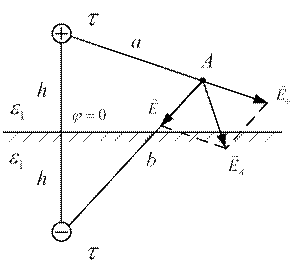
Применим метод зеркальных изображений. А напряженность поля и потенциал в точке А найдем, используя метод наложения
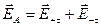 ;
;
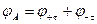 ;
;
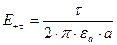 ;
; 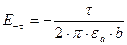 .
.
Примем точку с нулевым потенциалом на границе раздела под одним из проводов
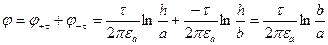 .
.
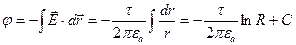 ;
;
для точки 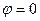 :
: 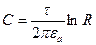 .
.
Определим силу притяжения провода к проводящей поверхности:
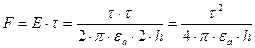 .
.
Поле заряженной оси, расположенной вблизи плоской границы раздела двух диэлектриков с различными диэлектрическими проницаемостями
(Диэлектрик - Диэлектрик)
В этом случае индуцированные на границе раздела не скомпенсированные связанные заряды влияют на поле в обеих сферах, для учета их вводят два фиктивных заряда. В данной задаче надо удовлетворить двум граничным условием.
а) Если реальный провод и исследуемая точка находятся в одной среде, то поле рассчитывают от двух зарядов: действительного 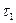 и зеркально отраженного фиктивного заряда
и зеркально отраженного фиктивного заряда 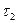 , все пространство заполнено диэлектриком, в котором находится исследуемая точка.
, все пространство заполнено диэлектриком, в котором находится исследуемая точка.
б) Если реальный провод и исследуемая точка находятся в разных средах, то поле в любой точке нижнего полупространства определяют как поле от некоторого дополнительного заряда 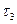 , расположенного в той же точке, где находился реальный заряд
, расположенного в той же точке, где находился реальный заряд  . Все пространство заполнено диэлектриком той среды, где находится исследуемая точка.
. Все пространство заполнено диэлектриком той среды, где находится исследуемая точка.
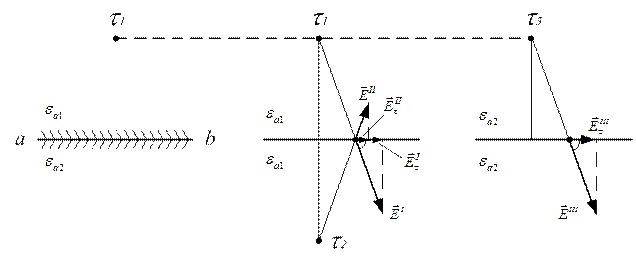
Из условия равенства тангенциальных составляющих напряженности поля:
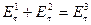 .
.
Из условия равенства нормальных составляющих вектора электрического смещения:
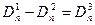 .
.
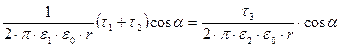 ;
;
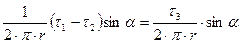 .
.
Решая совместно, получаем:
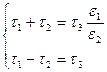 ;
;
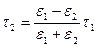 ;
; 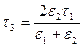 .
.
Знак 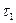 будет совпадать с
будет совпадать с 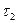 если
если 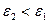 .
.
Знак 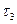 будет всегда как
будет всегда как 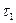 .
.
Пример:
Заряженная ось расположена в диэлектрике параллельно поверхности другого диэлектрика. Требуется определить напряженность электростатического поля и потенциал в точке А и В. Пусть 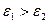 .
.
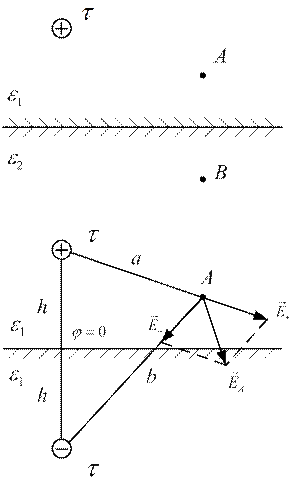
Рассмотрим точку А. Она лежит в одной среде с заряженной осью. Применяем метод зеркальных отражений. Все заполняем средой с диэлектрической проницаемостью 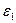 . Поле рассчитываем от двух зарядов: действительного
. Поле рассчитываем от двух зарядов: действительного 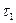 и зеркально отраженного фиктивного заряда
и зеркально отраженного фиктивного заряда 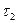 . Применим метод зеркальных изображений. Напряженность поля и потенциал в точке А найдем, используя метод наложения:
. Применим метод зеркальных изображений. Напряженность поля и потенциал в точке А найдем, используя метод наложения:
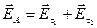 ;
;
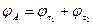 ;
;
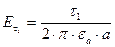 ;
; 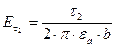 .
.
Примем точку с нулевым потенциалом на границе раздела под одним из проводов
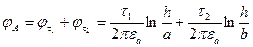 .
.
Рассмотрим точку В. Она лежит в разных средах с заряженной осью. Применяем метод зеркальных отражений. Все заполняем средой с диэлектрической проницаемостью 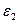 . Поле рассчитываем от фиктивного заряда
. Поле рассчитываем от фиктивного заряда 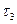 , расположенного в той же точке, где находился реальный заряд
, расположенного в той же точке, где находился реальный заряд 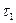 .
.
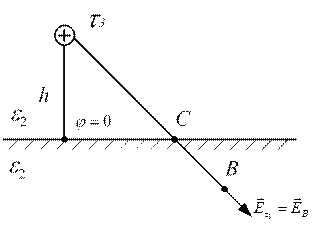
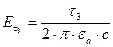 ;
;
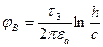 .
.
Замечание: если исследуемая точка лежит на поверхности провода, то расстояние от провода до исследуемой точки равно радиусу провода.
Точечный заряд вблизи границы
Диэлектрик – Проводник и Диэлектрик – Диэлектрик
Если поле создается не заряженной осью, а точечным зарядом, то вся методика расчетов сохраняется.
Пример.
Точечный заряд лежит вблизи границы диэлектрик – проводник. Найти напряженность и потенциал поля в точке А.
Применим метод зеркальных изображений.
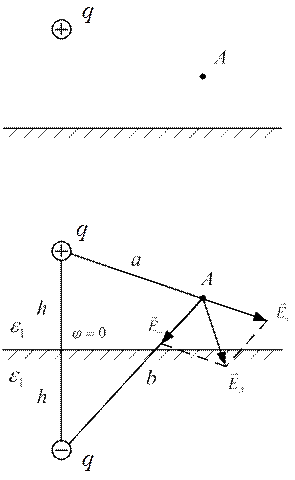
Напряженность и потенциал в точке А найдем, используя метод наложения:
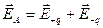 ;
;
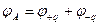 ;
;
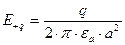 ;
; 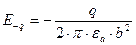 .
.
Примем точку с нулевым потенциалом на границе раздела под одним из проводов
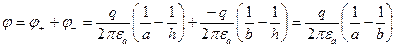 .
.
Определим силу притяжения провода к проводящей поверхности:
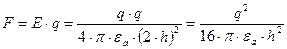 .
.
Пример.
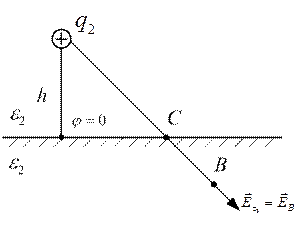
Точечный заряд лежит вблизи границы диэлектрик – диэлектрик. Требуется определить напряженность электростатического поля и потенциал в точке А и В. Пусть 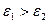 .
.
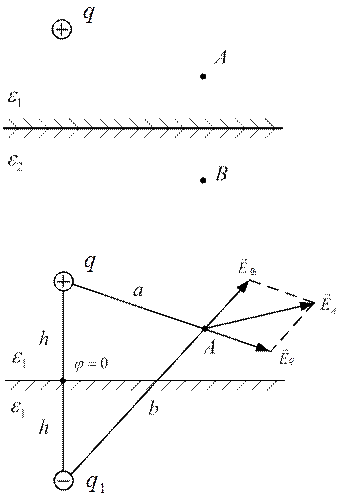
Рассмотрим точку А. Она лежит в одной среде с заряженной осью. Применяем метод зеркальных отражений. Все заполняем средой с диэлектрической проницаемостью 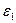 . Поле рассчитываем от двух зарядов: действительного
. Поле рассчитываем от двух зарядов: действительного 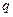 и зеркально отраженного фиктивного заряда
и зеркально отраженного фиктивного заряда 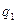 . Напряженность поля и потенциал в точке А найдем, используя метод наложения.
. Напряженность поля и потенциал в точке А найдем, используя метод наложения.
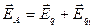 ;
;
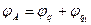 ;
;
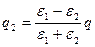 ;
;
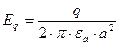 ;
; 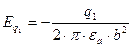 .
.
Примем точку с нулевым потенциалом на границе раздела под одним из проводов
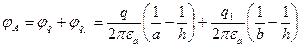
Рассмотрим точку В. Она лежит в разных средах с зарядом. Применяем метод зеркальных отражений. Все заполняем средой с диэлектрической проницаемостью 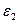 . Поле рассчитываем от фиктивного заряда
. Поле рассчитываем от фиктивного заряда 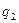 , расположенного в той же точке, где находился реальный заряд
, расположенного в той же точке, где находился реальный заряд 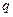 .
.
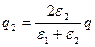 ;
;
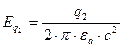 ;
;
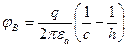 .
.
Дата добавления: 2020-10-14; просмотров: 648;











