Р. Нельсон и С. Уинтер: понятие рутины. Имитация и стохастика

Применяемые фирмами правила принятия решений образуют базисную рабочую концепцию как современной ортодоксальной теории, так и эволюционной. Однако основоположники эволюционной теории – Р. Нельсон и С. Уинтер – отвергают точку зрения, согласно которой поведение, максимизирующее прибыль, служит объяснением, почему правила принятия решений такие, каковы они есть. Они обходятся без всех трёх основных компонентов максимизирующих моделей[10]:

• глобальной целевой функции,
• точно определённого множества вариантов выбора,
• максимизирующего выбора как руководства к действиям фирмы.

Причём по их мнению «правила принятия решений» тесно связаны с «технологией» производства, тогда как с точки зрения ортодоксии это – совершенно разные вещи.

Общим термином для всех нормальных и предсказуемых образцов поведения фирм здесь выступает «рутина». Употребление данного термина охватывает характеристики фирм в диапазоне от вполне конкретных технических методов производства товаров и/или услуг до политики в области инвестирования, НИОКР или рекламы. В эволюционной теории эти рутины играют ту же роль, что и гены – в биологической эволюционной теории. Они наследуются в том смысле, что у организмов завтрашнего дня многие характеристики те же, что и у породивших их (например, благодаря строительству нового завода) организмов сегодняшних. Рутины подвержены отбору в том смысле, что организмы с определёнными рутинами могут функционировать лучше других, и если это так, то их относительная значимость в популяции (отрасли) возрастает со временем.

Выделяются три класса рутин с точки зрения породивших их эволюционных процессов:

1) Рутины, связанные с тем, что делает фирма в каждый момент времени при заданном наличном парке машин и оборудования и других факторах производства, объём которых нельзя легко увеличить за короткий срок (аналог краткосрочного периода у А. Маршалла). Таким образом, рутины, управляющие краткосрочным поведением, могут быть названы «функциональными характеристиками».

2) Это множество рутин определяет увеличение или снижение от периода к периоду основного капитала фирмы (т.е. факторов производства, постоянных на коротких промежутках времени). При этом в отдельных случаях принятие решения о строительстве нового завода может по существу не отличаться от принятия решения, продолжать ли эксплуатацию станка, который стал плохо работать или же остановить его и вызвать бригаду ремонтников. В таких случаях решения о строительстве завода следует относить к первому классу рутин. В другой же ситуации решение о новом заводе может быть похоже на решение осуществить крупную программу НИОКР на основе недавнего научно-технического открытия (т.е. менеджмент сталкивается с проблемой, которая не имела реальных прецедентов в прошлом, рассмотрение которой требует импровизированных процедур). Какой из этих двух стереотипов (первый или второй) будет применён, в большой степени зависит от соотношения между объёмами инвестиционного проекта и текущей хозяйственной деятельности фирмы.

3) Наконец, фирмы располагают рутинами, действие которых с течением времени модифицирует различные аспекты их функциональных характеристик. То есть существует некая иерархия правил принятия решений, в соответствии с которой процедуры более высокого уровня (например, обследование технологии производства, используемой на сегодняшний день или изучение ряда возможных изменений в политике рекламы) время от времени воздействуют на процедуры более низкого уровня (такие, как техника производства отдельных деталей или текущие правила принятия решений по поводу расходов на рекламу), видоизменяя последние.

Эти последние управляемые рутинами процессы изменения рутин моделируются как поиск. Предпринимается описание характеристик популяции модификаций рутин или новых рутин, которые может выявить поиск. Тактика предпринимаемого фирмой поиска характеризуется заданием распределения вероятностей того, что будет найдено в результате поиска, как функции от ряда переменных – например, от затрат фирмы на НИОКР, которые в свою очередь могут быть функцией от размера фирмы. У фирм предполагается наличие критериев оценки предлагаемых изменений рутин: практически во всех моделях таким критерием будет ожидаемая прибыль.

Эта концепция поиска является очевидным аналогом концепции мутации в биологической эволюционной теории. То, что при таком подходе поиск частично задаётся рутинами, которыми располагает фирма, соответствует принятому в биологической теории взгляду на мутации как на процесс, частично определяемый генетическим строением организма.

Рассмотрим модель выбора технологии индивидуальной фирмой.

Для простоты будем считать, что у всех технологий одинаковая капиталоёмкость и сосредоточимся на замещении переменных факторов производства. Сравним два режима постоянных цен на переменные факторы производства при различающихся относительных ценах. Формальный анализ ограничен случаем с двумя видами потребляемых факторов производства.

Пусть:

q – уровень выпуска;

k – основной капитал;

x₁, x₂ – объёмы двух видов переменных затрат;

k/q – постоянно для всех возможных технологий.

Технологии различаются коэффициентами затрат: a₁=x₁/q и a₂=x₂/q для двух видов переменных затрат. Поиск фирмы состоит в «вытягивании» из распределения альтернативных технологий a₁ и a₂ в окрестности её доминирующей технологии. Если найдена технология более дешёвая при доминирующих ценах w₁ и w₂, чем текущая, то есть если w₁·a^’₁ + w₂·a^’₂< w₁·a₁ + w₂·a₂, то фирма переходит к альтернативной технологии (a^’₁; a^’₂), в противном случае она останется при (a₁; a₂).

Основное допущение о распределении альтернатив, находимых в процессе поиска, состоит в том, что пропорциональные изменения коэффициентов затрат распределены независимо от доминирующих коэффициентов. Поэтому удобно описывать процесс в пространстве логарифмов коэффициентов затрат. А поскольку нас особенно интересует эволюция соотношений факторов производства, то удобно характеризовать технологию логарифмом отношения её коэффициентов:

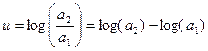
Чтобы задать положение технологии в двухмерном пространстве, нужна ещё одна координата, кроме u. Удобно задать эту вторую координату перпендикулярно первой, т.е. пусть это будет:

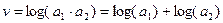
Соответственно, при заданной координате u технология с меньшей координатой v лучше, чем технология с большей координатой v. Геометрическое место точек в пространстве (a₁; a₂), на котором v постоянно, можно трактовать как изокванту производственной функции Кобба-Дугласа с равными показателями степени при двух факторах производства.

Будем рассматривать счётное упорядоченное множество возможных технологий, включающее конечную совокупность значений u, пронумерованных от 1 до N и бесконечно много значений v, пронумерованных от -∞ до +∞. Конкретнее, возможные технологии различаются по своим значениям u и v на целое, кратное константы Δ. Эта константа произвольна, и её роль можно было бы с равным успехом представить подходящим выбором для основания, по которому берутся логарифмы. Пусть u₁, u₂,… u_N и …v_-2, v_-1, v₀, v₁, v₂ … представляют собой разные возможные значения u и v. Под технологией (i,j) имеется в виду технология, характеризуемая парой:

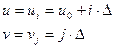
u₀ – константа, к которой привязан диапазон изменений рассматриваемых соотношений факторов производства, а Δ по существу соответствует пропорциональной разности между смежными в данном упорядоченном множестве коэффициентами затрат. Коэффициенты затрат технологии (i, j) это:

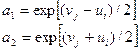
Рассмотрим это на графиках в пространствах (a₁; a₂) и 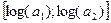соответственно.

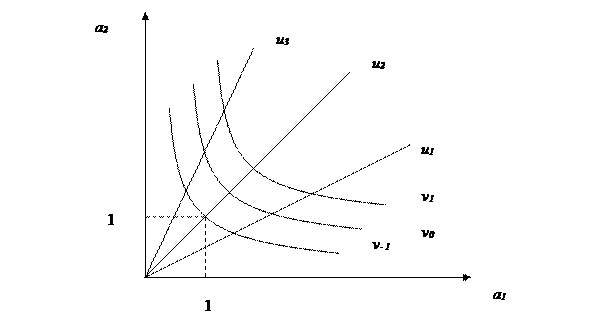
Рис. 3.1. Упорядоченное множество технологий в пространстве коэффициентов затрат

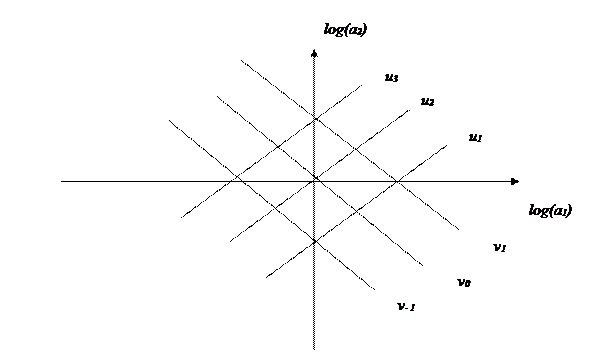
Рис. 3.2. Упорядоченное множество технологий в пространстве (log(a₁), log(a₂))

Теперь можно описать схему поиска. Пусть (i,j) – технология некоторой фирмы во время t, то есть:

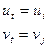
Результат поиска определяется парой случайных чисел (G_t, H_t), которая по существу представляет собой число шагов, проделанных фирмой по измерениям u и v при том ограничении, что u может варьировать только между u₁ и u_N :

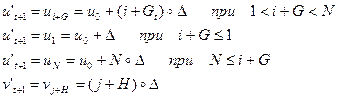
Случайные переменные (G_t, H_t) независимы от (u_t, v_t) и от всех предыдущих значений (u, v), они совместно распределены в ограниченной области –B≤(G, H)≤B, и их следует полагать индексированными как по номерам фирм, так и по периодам времени. Они распределены одинаково и независимо и по фирмам, и по времени. Если технология (u’_t+1, v’_t+1), полученная в результате поиска, выдерживает тест на уменьшение издержек, то u_t+1= u’_t+1, v_t+1= v’_t+1. В противном случае u_t+1= u_t, v_t+1= v_t.

Эта схема поиска и тестирования определяет распределение условных вероятностей технологий на период (t+1) при условии наличия технологии в период t, и это распределение зависит от распределения (G, H) и от цен факторов производства. При этом распределение альтернатив, обнаруженных поиском, предполагается независимым от цен факторов производства, но эти цены влияют на распределение принятых на вооружение альтернативных технологий посредством теста на сокращение издержек. Из сделанных допущений о независимости вытекает, что последовательность технологий, которые фирма применяет во времени, образует марковскую цепь. Существенное свойство этой цепи состоит в том, что последовательность соотношений факторов производства фирмы exp(u_t) сама является марковской цепью – фактически, конечной марковской цепью с постоянными во времени переходными вероятностями.

Итак, была рассмотрена реакция фирмы (и отрасли) на изменение рыночной конъюнктуры.

В ортодоксальной теории для характеристики этой реакции используются концепции «эластичности замещения» и «эластичности предложения». Они трактуются, как данные, определённые технологически, а не как переменные, которые можно объяснить при более глубоком структурном анализе. Эволюционная теория реакции фирмы и отрасли предполагает, что ответные реакции замещения и предложения должны быть функциями от количества и качества «поисковой» и «инновационной» деятельности, которую вызывает к жизни рост цен. Таким образом, некоторые ключевые параметры ортодоксальной теории в эволюционной теории становятся эндогенными.