Рост населения. Научно-технический прогресс
Базовая модель Солоу показывает, что само по себе накопление капитала не может объяснить непрерывный экономический рост. Высокий уровень сбережений временно увеличивает темпы роста, но экономика в конце концов приближается к устойчивому состоянию, при котором запасы капитала и объем производства постоянны. Для того, чтобы объяснить непрерывный экономический рост, который наблюдается в большинстве стран мира, нужно расширить модель Солоу и включить два других источника экономического роста: увеличение населения и технологический прогресс.
Вместо того, чтобы считать население постоянным, предположим, что население и рабочая сила растут с постоянным темпом прироста n. Как это повлияет на устойчивое состояние?
Изменение запасов капитала, приходящегося на 1-го работника, составит:
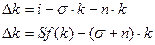
Составляющую 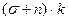 можно рассматривать как критическую величину инвестиций, т.е. инвестиции, необходимые для поддержания запаса капитала, приходящегося на 1 работника, на постоянном уровне.
можно рассматривать как критическую величину инвестиций, т.е. инвестиции, необходимые для поддержания запаса капитала, приходящегося на 1 работника, на постоянном уровне.
Если экономика достигла состояния устойчивости, инвестиции имеют две цели и две составляющие: во-первых, замена изнашиваемого капитала 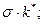 а во-вторых, обеспечение новых рабочих капиталом на уровне установившегося состояния
а во-вторых, обеспечение новых рабочих капиталом на уровне установившегося состояния 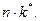
Рост населения дополняет исходную модель Солоу по трем направлениям:
1. Он позволит приблизиться к объяснению причин экономического роста. В устойчивом состоянии экономики при растущем населении и выпуск продукции на 1-го работника, и объем капитала на 1-го работника остаются неизменными, но поскольку число работников растет с темпом прироста n, капитал и объем производства тоже растут с темпом прироста n. Рост населения не может объяснить длительного роста уровня жизни, но объясняет непрерывный рост валового выпуска продукции.
2. Рост населения позволяет дать дополнительные объяснения того, почему некоторые страны богаты, а другие бедны. Увеличение темпа прироста населения (n2 > n1) сдвигает влево/вверх линию, представляющую рост населения и износ на Рис. 1.9. Для нового устойчивого уровня характерен меньший запас и капитала на 1-го работника. Отсюда модель Солоу предсказывает, что страны с более высоким темпом прироста населения будут иметь меньшую фондовооружённость и, следовательно, меньшие доходы.
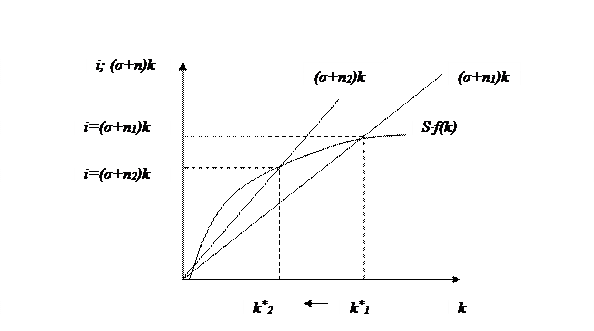
Рис. 1.9. Рост населения
3. Рост населения влияет на уровень накопления капитала по золотому правилу. Поскольку устойчивый объем производства 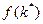 , инвестиции в устойчивом состоянии
, инвестиции в устойчивом состоянии 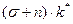 , то устойчивый уровень потребления
, то устойчивый уровень потребления 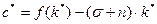 . Уровень
. Уровень 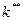 , который максимизирует потребление, таков, что
, который максимизирует потребление, таков, что 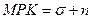 или
или 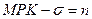 , то есть чистый предельный продукт капитала равен темпу прироста населения.
, то есть чистый предельный продукт капитала равен темпу прироста населения.
Включим в модель Солоу технический прогресс – третий источник экономического роста. Запишем производственную функцию следующим образом:
Y=F(k; L·E),
где Е – представляет собой новую переменную, которую мы назовем эффективностью труда 1-го работника. Составляющая L·E – переменная, измеренная в единицах труда с постоянной эффективностью. Принимается во внимание количество работников L, эффективность труда каждого из них равна Е. В соответствии с новой производственной функцией общий объем производства Y зависит от количества единиц капитала К и от числа эффективных единиц рабочей силы L·E.
Простейшим допущением относительно технического прогресса является то, что он вызывает увеличение эффективности труда Е с постоянным темпом прироста g. Например, если g = 0,02, то отдача от каждой единицы труда возрастает так, как если бы рабочая сила за год возросла на 2%. Эта форма технического прогресса называется трудосберегающей.Поскольку рабочая сила L растёт с темпом прироста n и отдача от каждой единицы труда Е растет с темпом прироста g, общее количество эффективных единиц труда L·E увеличивается с темпом прироста n+g.
Описание технического прогресса через приращение эффективности труда делает его аналогичным росту населения. Пусть k = K/L·E, т.е. капитал на единицу труда с постоянной эффективностью (например, начальная Е=1). у=Y/L·E. Используя эти определения, можно записать у=f(k). Анализ происходит по той же схеме, что и в случае с ростом населения. Уравнение, показывающее изменение k с течением времени, теперь выглядит следующим образом:
Δk = S·f(k) – (σ+n+g)·k
Если величина g растет быстро, то и общее количество единиц труда с постоянной эффективностью растет быстро, а прирост капитала на такую единицу труда сравнительно мал, то, как следствие, прирост фондовооружённости даже может стать отрицательным.
| Трудосберегающая форма технического прогресса одновременно с ростом производительности может вызывать, при низком общем росте инвестиций, снижение потребности в рабочей силе. Это обстоятельство обусловило пафос теоретической модели экономического роста К. Маркса, рассматриваемой в следующей лекции. |
Устойчивый рост в модели Солоу с учетом технического прогресса
| Переменные | Обозначения | Темп прироста |
| 1) Капитал на единицу труда с постоянной эффективностью | k = К/Е·L | |
| 2) Объем производства на единицу труда с постоянной эффективностью | y=(Y/E·L)=f(k) | |
| 3) Объем производства на 1 работника | Y/L = y·E | g |
| 4) Общий объем производства | Y = y·(E·L) | n+g |
Таким образом, с учетом технического прогресса модель Солоу позволяет объяснить, почему уровень жизни растет из года в год. Технический прогресс может поддерживать непрерывный рост выпуска продукции на 1 работника; тогда как высокий уровень сбережений ведет к высоким темпам прироста только до момента достижения устойчивого состояния. Модель Солоу показывает, что только технический прогресс может объяснить непрерывно растущий уровень жизни.
Введение в модель технического прогресса также изменяет условия выполнения Золотого правила:
с* = f(k*) – (σ + n + g)·k*
Устойчивый уровень потребления с* будет максимальным, если:
МРК – σ = n + g
Таким образом, при запасе капитала по Золотому правилу чистый предельный продукт капитала МРК – σ равен сумме темпов прироста населения и темпов прироста объемов производства на 1 работника.
Дата добавления: 2016-07-22; просмотров: 2580;











