Накопление капитала

Рассмотрим обычную производственную функцию, описывающую зависимость дохода и затрат:

.

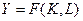Допустим, что функция однородна в первой степени, или обладает свойством постоянной отдачи от масштаба:

.

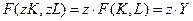Обозначим:

y=Y/L – выпуск продукции на одного работника (производительность);

k=K/L – капитал (фонды), приходящиеся на одного работника (фондовооруженность).

Рассмотрим взаимосвязь производительности и фондовооруженности:

.

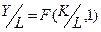(очевидно, z=1/L).

Тогда производственную функцию можно переписать следующим образом:

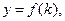где .

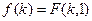Рассмотрим ее график:

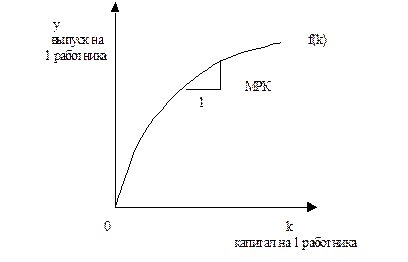
Рис.1.1 График производственной функции

Тангенс угла наклона данной производственной функции показывает, сколько дополнительного продукта на одного работника можно получить, если увеличить фондовооруженность на одну единицу. Эта величина является предельным продуктом капитала МРК. Формально можно записать:

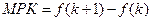
По мере возрастания k наклон графика уменьшается, что отражает посылку о снижении предельной производительности.

Перейдем к рассмотрению потребления:

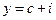
Продукция, произведенная каждым работником, делится между потреблением, приходящимся на одного работника, и инвестициями в расчете на одного работника.

В модели Солоу предполагается, что функция потребления имеет следующую форму:

,

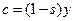где норма сбереженияs принимает значения от 0 до1.

Подставляя значение функции потребления в предыдущее выражение, получаем:

.

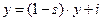Отсюда инвестиции, как и потребление, изменяются прямо пропорционально доходу:

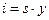
Но если инвестиции равны сбережениям, то норма сбережений S также показывает, какая часть произведенной продукции направляется на капитальные вложения.

Представив две главные составляющие модели Солоу – производственную функцию и функцию потребления – можно проанализировать, как накопление обеспечивает экономический рост. Запасы капитала могут изменяться по двум причинам:

1) инвестиции приводят к росту запасов капитала;

2) часть капитала изнашивается, что приводит к уменьшению запасов капитала.

Для того чтобы понять, как изменяются запасы капитала, необходимо найти факторы, определяющие величину инвестиций и выбытия капитала.

Инвестиции в расчете на одного работника являются частью продукта, приходящегося на одного работника (другими словами, фондовооруженность – это часть производительности) – sy. Заменив y на выражение производственной функции, представим инвестиции на одного работника как функцию от фондовооруженности:

Чем выше уровень фондовооруженности k, тем выше объем производства f(k) и больше инвестиции i:

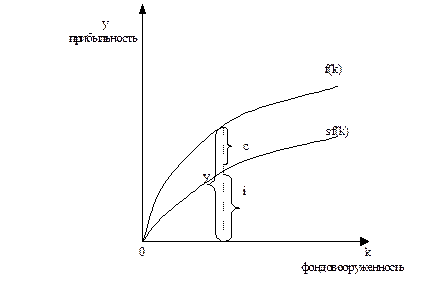
Рис. 1.2. Потребление и инвестиции как функции от фондовооруженности.

Норма сбережений (S) определяет деление произведенного продукта y на потребление (c) и инвестиции (i). Для любого уровня капиталовооруженности k объем производства есть f(k), инвестиции равны s×f(k), а потребление f(k)-s×f(k).

Чтобы учесть в модели выбытие капитала, предположим, что ежегодно выбывает определенная доля капитала s. Назовем s нормой выбытия[1]. Например, если капитал эксплуатируется в среднем 25 лет, то норма выбытия равна 4% в год (s=0,04). Таким образом, количество капитала, которое выбывает каждый год, составляет s×k.

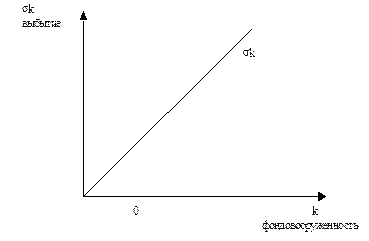
Рис. 1.3. График функции выбытия капитала

Ежегодно выбывает определенная фиксированная часть капитала, поэтому выбытие пропорционально запасам капитала.

Влияние инвестиций и выбытия на запасы капитала можно выразить с помощью следующего уравнения:

,

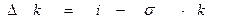
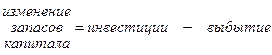где Dk – изменение запасов капитала, приходящихся на одного работника в год.

Поскольку инвестиции равны сбережениям, изменение запасов капитала можно записать следующим образом:

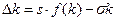
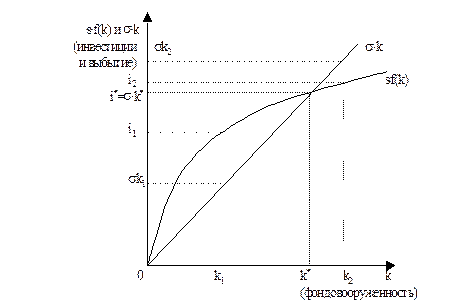
Рис.1.4. График функции выбытия капитала и функции инвестиций

Поскольку норма сбережений S постоянна, и сбережения равны инвестициям, объем инвестиций равен s×f(k). Поскольку капитал выбывает с постоянной скоростью s, то объем выбытия есть s×k.

Устойчивый уровень k^* -это такая фондовооруженность работников, при которой инвестиции равны выбытию, в точке k^* обе кривые пересекаются. При k>k^* инвестиции меньше выбытия, и запасы капитала уменьшаются; при k<k^* инвестиции превышают выбытие, и запасы капитала растут.

Устойчивый уровень фондовооруженности соответствует равновесию экономики в долгосрочном плане. Независимо от первоначального объема капитала, с которым экономика начинает развиваться, она затем достигает устойчивого состояния.

Что будет происходить, если изменится норма сбережений (норма накопления)?

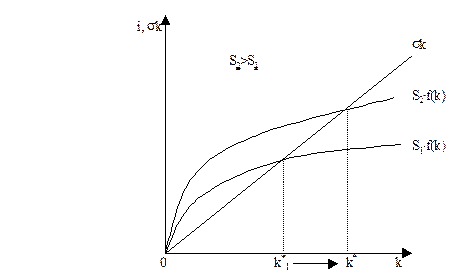
Рис. 1.5. Изменение объема инвестиций при изменении нормы накопления

Рост нормы сбережений S показывает, что размер инвестиций при любых уровнях капиталовооруженности станет больше. В точке прежнего устойчивого состояния инвестиции теперь превосходят выбытие. Запасы капитала растут, пока экономика не достигнет нового устойчивого состояния – с большей капиталовооруженностью и прибыльностью.

Модель Солоу показывает, что норма сбережений является ключевым фактором, определяющим величину устойчивой фондовооруженности. Если норма сбережений более высока, то экономика будет иметь при прочих равных условиях больший запас капитала и более высокий уровень производства.