Коэффициенты, оценивающие несинусоидальные функции

В электротехнике в технических расчетах используют коэффициенты, оценивающие несинусоидальность токов и напряжений:

1. Коэффициент формы: 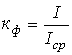. Оценивает, насколько искажена форма периодической функции по отношению к синусоидальной.

2. Коэффициент амплитуды: 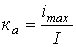. Этот коэффициент показывает, во сколько раз максимальное значение периодической функции превышает амплитуду основной гармоники.

3. Коэффициент искажений: 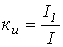. Этот коэффициент показывает, во сколько раз действующие значение отличается от действующего значения первой гармоники.

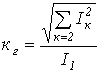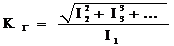4. Коэффициент гармоник: или . Этот коэффициент показывает отношение всех бесполезных гармоник к первой гармонике.

5. Коэффициент мощности:

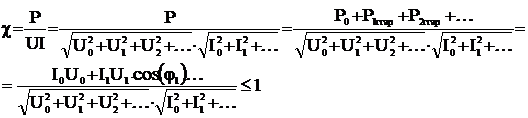
Этот коэффициент определяет отношение суммарной активной мощности периодической функции к её полной мощности.

В линейных электрических цепях гармонического тока существует понятие мощности:

.

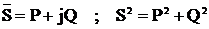Если же цепь не синусоидальная, то нарушается последнее равенство:

.

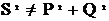Обычно правая часть становится больше левой. Равенство восстанавливается введением новой величины (Т):

,

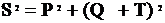где Т – реактивная мощности искажений, тогда:

.

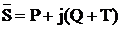Это и есть мощность в цепи с несинусоидальными токами.

Несколько слов о несинусоидальности токов в цепях. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.

На практике к несинусоидальности напряжений и токов следует подходить двояко:

· в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов;

· в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями.

В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данном разделе будут рассматриваться цепи только с периодическими переменными.

Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами.

В качестве примера на рис. 5.4,а представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (см. рис. 5.4,б).

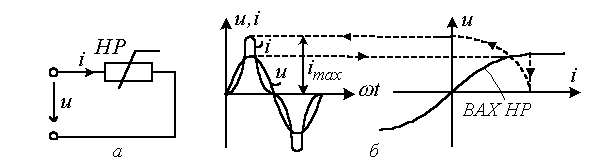
Рис. 5.4

Контрольные вопросы к теме

1. В каком случае прибегают к разложению исходной функции в ряд Фурье? Какие два вида записи существуют для рядов Фурье.

2. Как определяются коэффициенты гармонических составляющих ряда Фурье? Какие виды симметрии существуют и к чему они приводят?

3.Как определяется действующее и среднее значения негармонической периодической величины тока или напряжения.

4. Какие существуют коэффициенты, оценивающие несинусоидальность исходных функций тока или напряжения?

5. Как определяется мощность в цепи не гармонического тока, что такое мощность искажения?