Разложение периодической функции в ряд Фурье
Из математики известно, что всякая периодическая функция 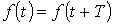 , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
, где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом:
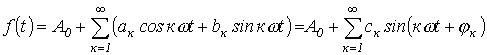 . .
| (1) |
| |
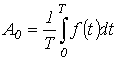 - постоянная составляющая или нулевая гармоника;
- постоянная составляющая или нулевая гармоника; 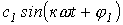 - первая (основная) гармоника, изменяющаяся с угловой частотой
- первая (основная) гармоника, изменяющаяся с угловой частотой 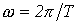 , где Т – период несинусоидальной периодической функции.
, где Т – период несинусоидальной периодической функции.
В выражении (1) 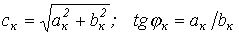 , где коэффициенты
, где коэффициенты 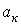 и
и 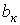 определяются по формулам
определяются по формулам
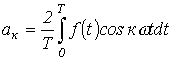 ;
; 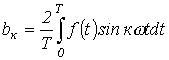
5.2. Свойства периодических кривых, обладающих  симметрией
симметрией
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры
Рис. 5.1
гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях.
1. Нечетная симметрия: кривые, симметричные относительно оси абсцисс (Рис. 5.1).


Рис.5.2 Рис. 5.3
К данному типу относятся кривые, удовлетворяющие равенству 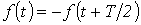 . В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е.
. В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е. 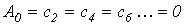 .
.
2. Четная симметрия: кривые, симметричные относительно оси ординат.
К данному типу относятся кривые, для которых выполняется равенство 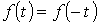 ( рис.5.2). В их разложении отсутствуют синусные составляющие, т.е.
( рис.5.2). В их разложении отсутствуют синусные составляющие, т.е. 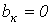 .
.
3. Косая симметрия: кривые, симметричные относительно начала координат.
К этому типу относятся кривые, удовлетворяющие равенству 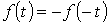 (рис.5.3). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е.
(рис.5.3). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е. 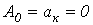 .
.
Дата добавления: 2020-10-14; просмотров: 621;











