Выражение ошибки численного решения через изменение корней характеристического уравнения

Приведем матрицу A к диагональному виду [2.6]:

A = S L S-1 (2.1.15)

Здесь L –диагональная матрица, составленная из собственных значений Zkматрицы А, являющихся корнями характеристического уравнения

det(I 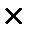Z – A ) = 0 , (2.1.16)

S - диагонализирующая матрица, составленная из собственных векторов матрицы А.

Известно, что диагонализирующая матрица S сохраняет свой вид для любой степени А и для любого матричного полинома по степеням А, включая сходящиеся степенные ряды. Диагонализируя матричную экспоненту (4) и умножая ее слева на S-1и справа на S, получим:

eLh= I + Lh + (Lh)2/2 + …+ (Lh)r/r! + (Lh)r+1/(r+1)! +…

(2.1.17)

Здесь eLh– диагональная матрица со скалярными экспонентами

eZkhпо диагонали.

Диагонализируя соотношения (6) и умножая их слева на S-1и справа на S, получим:

eLh= eLh+ deLh, eLh= I+Lh+L2h2…(Lh)r/r! ,

(2.1.18)

deLh= (Lh)r+1)/(r+1)! + …

Все матрицы в (18) диагональные.

Диагонализируем соотношение (12):

e(L+dL)h= eLh (2.1.19)

Напомним, что матрица dA в (12) характеризует ошибку численного решения в области коэффициентов решаемого уравнения (1).

Аналогично, диагональная матрица dL из (19) характеризует ошибку численного решения в области корней характеристического уравнения (16). Точное решение (19) относительно dL имеет вид:

dL = ln(eLh)/h – L (2.1.20)

Диагонализируя (13), получим другю форму точного решения (19):

edLh– I = - e-LhdeLh (2.1.21)

В (20) и (21) все матрицы диагональные, поэтому эти соотношения верны для любой строки, то-есть для любого корня характеристического уравнения (16). Учитывая вышесказанное и разлагая входящие в (21) экспоненты в степенные ряды, можно получить приближенные скалярные выражения разной степени точности:

dZkh 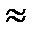- (Zkh)r+1[1 – Zkh(r+1)/(r+2) +…]/(r+1) dZkh 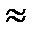- (Zkh)r+1/(r+1)! (2.1.22)

Как видно из выражений (20) - (22), смещение dZk зависит только от

k -того корня Zkи не зависит от других корней характеристического уравнения.

Таким образом, численное решение системы дифференциальных уравнений (1) с корнями характеристического уравнения

Z1, ..., Zn эквивалентно точному решению другой системы уравнений со смещенными корнями Zk+ dZk, k = 1,…n, где смещения корней определяется соотношениями (2.1.20)…(2.1.22).

Если по условиям решаемой задачи можно сформулировать

допустимые изменения корней dZkхарактеристического уравнения, то соотношения (2.1.20) …(2.1.22) позволят осуществить предварительный выбор порядка метода r и шага дискретизации h.