Практическая реализация метода SYSTEMA

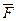Матрице поставим в соответствие нижнюю треугольную матрицу с элементами

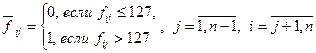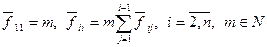, (7.17)

Выбор 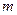призван обеспечить для матрицы 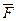наличие свойств, близких к (7.15).

Формирование вектора правой части СЛАУ для определения 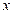происходит следующим образом:

1. Вычисляется вектор 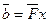, 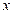есть решение СЛАУ

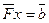(7.18)

За счет (7.17) элементы 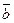могут оказаться достаточно большими.

1. По 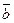генерируется вектор 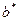по следующему правилу:

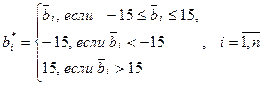, (7.19)

а СЛАУ (7.18) для восстановления 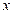заменяем на систему 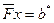. Поскольку 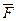является нижней треугольной, то количество арифметических операций при решении 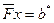определяется как 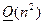. Эта цель преследовалась при кодировании матрицы исходного изображения матрицей треугольного вида.

Остановимся более подробно на целесообразности формирования 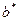в соответствии с (7.19). Кодирование матрицей 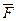, в основном, уменьшает значения элементов матрицы, что дает возможность соответствующего уменьшения и элементов вектора 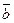= 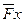по сравнению с 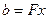(конечно, если 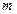не очень велико), однако все же не гарантирует их малости. Если в качестве правой части системы, используемой для восстановления 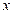, рассматривать 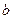(СЛАУ (7.2)) или 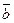(СЛАУ (7.18)), то перед погружением такого вектора для обеспечения надежности восприятия после встраивания, очевидно, потребуется какой-либо способ его кодирования, например, перевод в бинарную последовательность, что может значительно увеличить длину погружаемой числовой последовательности. Это приведет к некорректности сравнения результатов декодирования 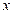при его непосредственной и опосредованной, при помощи правой части системы, пересылке. Следовательно, элементы погружаемого вектора должны быть настолько малыми, чтобы избежать необходимости какого-либо кодирования для уменьшения мощности множества, содержащего их возможные значения. Однако при выборе конкретных пороговых значений в (7.19), 15 и -15, учитывается не только это требование, к которому еще вернемся ниже.

При практической реализации метода встает вопрос выбора значения параметра 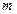. Очевидно, 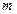для обеспечения устойчивости декодирования должно быть как можно больше, хотя реально не может увеличиваться до бесконечности; с другой стороны, 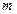непосредственно участвует в формировании элементов вектора 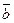, по которому генерируется 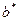. Чем больше будет 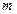, тем больше будут значения элементов 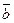, тем большее возмущение получит вектор 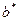на этапе формирования и, если бы речь шла о классическом решении СЛАУ, то такие возмущения могли бы привести к неприемлемой погрешности декодирования даже с учетом малого числа обусловленности Скила матрицы системы. Однако, как будет показано ниже, используемый подход к решению системы позволяет уйти от отрицательных последствий возмущения вектора правой части на этапе формирования. Таким образом, приоритетным остается обеспечение устойчивости декодирования за счет выбора .

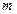После формирования вектора 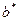, он погружается в матрицу ОС. При пересылке СС подвергается возмущающим воздействиям в канале связи. Выделение информационного вектора 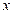происходит при решении СЛАУ

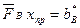, (7.20)

где 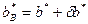— возмущенный вектор ;

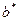матрица 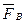получается по возмущенной матрице 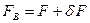ОС аналогично (7.17).

Для большинства изображений при малых возмущениях в канале связи 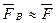, а 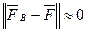. Действительно, отличие этих матриц может быть в элементах, являющихся результатом кодирования элементов исходной матрицы, значения которых находятся в окрестности 127. Таким образом, можно считать, что система (7.20) отличается от системы (7.18) лишь вектором правой части.

В любом случае, очевидно, 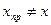. Учитывая вид множества, которому принадлежат элементы 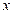, для осуществления окончательного декодирования по имеющемуся вектору 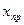целесообразно использовать формулу

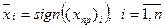. (7.21)

Вектор 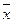назовем sign-решением системы (7.20), а непосредственную реализацию алгоритма, предложенную выше и использующую (7.21), будем называть СМ-SIGN (реализация СМ sign-решения системы). Использование формулы (7.21) при декодировании допускает неограниченно большие погрешности при решении (7.20), которые никак не повлияют на результат декодирования, т.е. 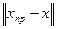может быть сколь угодно велика, если при этом выполняются условия: 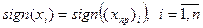. Таким образом, возмущения правой части системы при формировании 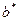, о которых говорилось выше, сохраняющие знаки элементов вектора решения, не отражаются на результате декодирования, проводимого в соответствии с (7.20), (7.21). Такой подход к решению системы является новым и никогда ранее не рассматриваемым, имеющий простую геометрическую интерпретацию. Вектор 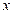с элементами из множества 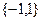, однозначно определяет координатный ортант в пространстве 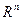, его содержащий. Координаты любого вектора 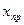, принадлежащего этому же ортанту, будут иметь те же знаки, что и соответствующие координаты вектора 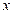, а значит при использовании для окончательного декодирования формулы (7.21) определят элементы вектора 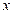точно, независимо от реального отклонения 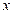от 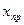. Кроме того, предложенный подход к решению системы допускает возможность правильного решения даже при неограниченно большом возмущении вектора правой части. Действительно, геометрически решение СЛАУ — это пересечение 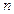плоскостей 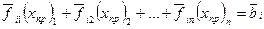, , 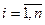в 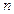-мерном пространстве. Возмущение элемента 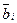в процессе его замены на 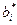в правой части 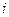-го уравнения системы 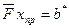, приведет к параллельному переносу соответствующей плоскости 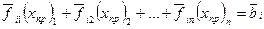вдоль ее вектора нормали 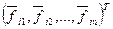на величину 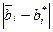в каком-либо из двух возможных направлений. Величины этих параллельных переносов могут быть неограниченно большими и при этом оставлять точку пересечения плоскостей в определенном координатном ортанте. Наглядная иллюстрация сказанному приведена на рис.7.1 для , .

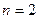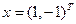Такой подход к решению системы дает возможность, как показывают результаты вычислительного эксперимента, приведенные ниже, получить большой объем 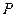правильно восстановленной информации даже при больших возмущениях входных данных, т.е. предлагаемая реализация метода SYSTEMA может обеспечивать его устойчивость по отношению даже к неограниченно большим возмущающим воздействиям, что невозможно обеспечить при непосредственной пересылке вектора секретной информации. При геометрической интерпретации очевидной становится значимость конкретных направлений этих возмущений: если возмущения вектора правой части в рассмотренном примере приведут к параллельному переносу плоскостей, отвечающих уравнениям СЛАУ, вдоль векторов нормалей, но в противоположных к указанным на рис.7.1 направлениям, то и сравнительно небольшие возмущения выведут точку пересечения плоскостей за пределы четвертого квадранта, т.е. приведут к ошибкам при декодировании ДИ на втором этапе метода SYSTEMA.

Заметим, что предложенный подход, основанный на вычислении sign-решения системы, является практическим использованием знаковой чувствительности вектора-решения, может быть применен при моделировании процессов, чувствительность которых различна к различным возмущающим воздействиям, кроме того, при геометрическом моделировании объектов, в том числе и объектов информационной безопасности, результат возмущения которых зависит от направления возмущающего воздействия.

Недостатком предлагаемого метода SYSTEMA остается ограниченность пропускной способности, поскольку длина информационного вектора 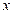не превосходит 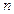. Увеличение объема передаваемой информации может быть достигнуто следующим образом.

Пусть матрица размерности 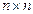отвечает ОС. Разобьем ее стандартным образом на квадратные блоки фиксированного малого размера, например, 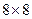. Пусть — один из таких блоков. К каждому из блоков применим предложенный выше СМ-SIGN. Заметим, что количество арифметических операций при работе с — константа, не зависящая от размерности матрицы исходного изображения. Обозначим ее 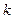. Количество блоков определяется как 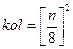, тогда общее количество арифметических операций при работе со всем изображением равно 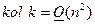, а суммарный объем погружаемой информации определится как 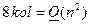, т.е. оказывается на порядок больше, чем при рассмотрении матрицы изображения целиком.

Такую модификацию предложенного метода далее будем называть блоковой реализацией СМ sign-решения системы (БСМ-SIGN).

Основной целью вычислительного эксперимента является практическое подтверждение теоретически обоснованной большей устойчивости к возмущающим воздействиям в канале связи предложенного СМ с двухэтапным декодированием по сравнению с методом, использующим непосредственную пересылку информационного вектора. Критерием для такого сравнения является объем правильно восстановленной информации в том и другом случае при одинаковых условиях проведения эксперимента.

Вычислительный эксперимент проводился в среде MATLAB. Возмущения в канале связи моделировались при помощи аддитивного гауссовского шума, наложение которого осуществлялось стандартной процедурой imnoise, со следующими параметрами: математическое ожидание полагалось везде равным нулю, а σ принимало значения 0.0001, 0.0005, 0.0008, 0.001, 0.01. Дальнейшее увеличение уровня шума приводило к потере информативности возмущенного изображения и поэтому не рассматривалось.

Для демонстрации результатов эксперимента выбраны два изображения, используемые в качестве ОС: POUT (рис.7.2(а)) и SATURN (рис.7.3). Выбор сделан не случайно. Непосредственно устанавливается, что матрица первого изображения является хорошо обусловленной, а число обусловленности матрицы второго изображения бесконечно большое.

Погружение ДИ в ОС проводилось в пространственную область аддитивно в выделенный предварительно контур, причем непосредственное погружение 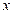и погружение 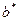происходило в одни и те же пиксели контура. В СМ-SIGN пороговые значения -15 и 15 в формуле (7.19) определялись экспериментально, исходя, во-первых, из требования обеспечения надежности восприятия после погружения ДИ (рис.7.2(б)), а также с учетом особенности, о которой будет сказано ниже. На полученные СС накладывался шум с одинаковыми параметрами (рис.7.2(в)), после чего происходило одноэтапное или двухэтапное (СМ-SIGN) декодирование вектора 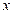(декодирование 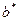проводилось тем же способом, что и ).

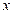а б в

Рис.7.2. Исходное изображение POUT (а); стеганосообщение, сформированное СМ-SIGN (б); стеганосообщение, претерпевшее возмущение в виде аддитивного гаусовского шума, используемое для декодирования (в)

В результате вычислительного эксперимента была установлена зависимость между уровнем возмущающих воздействий в канале связи и объемом правильно восстановленной информации 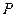, а также практически подтверждена независимость результатов работы SYSTEMA от реальных свойств матрицы ОС. Увеличение объема 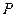достигалось путем варьирования 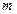. Результаты проведенного исследования представлены на графиках зависимости 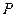от уровня шума, характеристикой которого является среднеквадратичное отклонение, при различных значениях 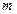(рис.7.4). Для построения графиков каждый из экспериментов состоял из 100 независимых опытов, определяемых одинаковыми параметрами. В качестве результата эксперимента ( 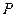при заданном шуме и значении 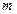) бралось среднее арифметическое значение по всем 100 опытам.

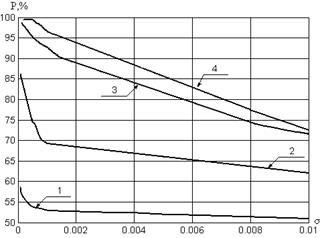
Результат работы СМ-SIGN, как и ожидалось, в силу виртуального моделирования свойства (7.15) для матрицы системы, не зависит от реальных свойств матрицы изображения, используемого в качестве ОС (рис.7.4). СМ-SIGN может использоваться для ОС с произвольной матрицей и является более устойчивым к возмущениям в канале связи по сравнению с алгоритмом, осуществляющим непосредственную пересылку информационного вектора, даже при достаточно малых значениях .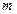

а б

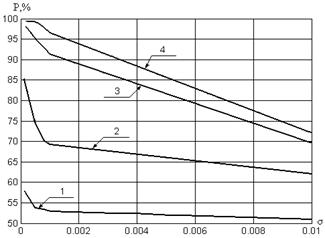
Рис. 7.4. Зависимость 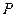:ОС — SATURN (а); ОС — POUT (б)

1 — непосредственная пересылка и декодирование ;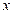

2 — СМ-SIGN при 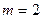; 3 — СМ-SIGN при 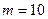; 4 — СМ-SIGN при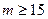

Интересным является тот факт, что, как показывает эксперимент, кривая 4 на рис.7.4(а),(б), построенная для 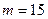, не будет изменяться при дальнейшем увеличении значения 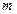. Этот странный на первый взгляд факт легко объясняется, исходя из особенностей выбранного метода решения СЛАУ. Поскольку нас интересуют знаки элементов вектора, получаемого при решении (7.20), то определяющим фактором успешного декодирования является сохранение знаков в векторе 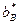по сравнению с 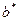. Однако, как только диапазон возможных значений 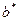перекроется шумом, нужные для декодирования знаки будут безвозвратно утеряны. И тут уже абсолютно не важно, насколько большим будет взято 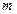. На итоговые значения 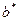это никак не повлияет (при достаточно больших 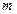все элементы 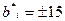). Дальнейшее увеличение процента правильно восстановленной информации для достаточно большого квадратичного отклонения, характеризующего шум (возмущающие воздействия в канале связи), можно осуществить только путем расширения границ множества значений элементов 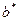, однако это недопустимо при выбранном способе погружения (модули пороговых значений, равные 15, как установлено экспериментально, невозможно более увеличить, не нарушая требования надежности восприятия).

Реализация БСМ-SIGN, дающая возможность на порядок увеличить пропускную способность, не изменила качественной картины работы сравниваемых методов, описанной выше, как и можно было предположить заранее. Результаты нашли свое отражение на рис.7.5 для изображения POUT (для изображения SATURN картина идентична).

Таким образом разработка и практическая реализация СМ SYSTEMA, дала возможность подтвердить достижение большей устойчивости метода к возмущающим воздействиям в канале связи, по сравнению с методом, основанным на непосредственной пересылке и декодировании информационного вектора. Ценность СМ-SIGN заключается в том, что он может быть использован для произвольного ОС, а свойства матрицы этого ОС не влияют на результат декодирования.

Предложенная численная реализация метода требует 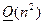арифметических операций, где 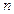— размерность матрицы СЛАУ.

Вопросы

1. Как определяется объем правильно восстановленной информации?

2. Какая задача называется чувствительной к возмущающим воздействиям?

3. Когда стеганосообщение называется чувствительным к возмущающим воздействиям?

4. Что такое число обусловленности задачи?

5. Что является мерой чувствительности задачи к возмущающим воздействиям?

6. В чем состоит основная идея метода SYSTEMA двухэтапного декодирования дополнительной информации?

7. За счет чего повышается эффективность декодирования стеганографического алгоритма при использовании его совместно с SYSTEMA?

8. Условие устойчивости метода SYSTEMA.

9. Как для матрицы определяется число обусловленности Скила?

10. Как обеспечить малое число обусловленности Скила матрицы произвольного изображения? Всегда ли это можно сделать?

11. Понятие sign-решения системы линейных уравнений. Что обеспечивает sign-решение для системы?

12. Основной недостаток метода SYSTEMA.

13. Оценка вычислительной сложности метода SYSTEMA.

Литература

1. Кобозєва А.А. Аналіз захищеності інформаційних систем / Кобозєва А.А., Хорошко В.А., Мачалін І.О. – К.: Вид.ДУІКТ, 2010. – 316 с.

2. Кобозева А.А. Анализ информационной безопасности / А.А.Кобозева, В.А.Хорошко. – К.: Изд. ГУИКТ, 2009. – 251 с.

3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с.

4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с.

5. Гонсалес Р. Цифровая обработка изображений / Р.Гонсалес, Р.Вудс; пер. с англ. под ред. П.А.Чочиа. — М.: Техносфера, 2005. — 1072 с.

6. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.

7. Гантмахер Ф.Р. Теория матриц / Ф.Р.Гантмахер. — М.: Наука, 1988. — 552 с.

8. Грибунин В.Г. Цифровая стеганография / В.Г.Грибунин, И.Н.Оков, И.В.Туринцев. — М.: Солон-Пресс, 2002. — 272с.

9. Стеганография, цифровые водяные знаки и стеганоанализ : [монография] / А.В. Аграновский, А.В. Балакин, В.Г. Грибунин, С.А. Сапожников. — М.: Вузовская книга, 2009. — 220 с.

10. Кобозева А.А. Применение сингулярного и спектрального разложения матриц в стеганографических алгоритмах / А.А.Кобозева // Вісник Східноукр-го нац-го ун-ту ім. В.Даля. — 2006. — №9(103), ч.1. — С.74—82.

11. Конахович Г.Ф. Компьютерная стеганография. Теория и практика / Г.Ф.Конахович, А.Ю.Пузыренко. — К.: МК — Пресс, 2006. — 288 с.

12. Кобозева А.А. Учет свойств нормального спектрального разложения матрицы контейнера при обеспечении надежности восприятия стегосообщения / А.А.Кобозева, Е.А.Трифонова // Вестник НТУ «ХПИ». — 2007. — №18. — С.81—93.

13. Кобозева А.А. Оценка чувствительности стегосообщения к возмущающим воздействиям / А.А.Кобозева, Е.В.Нариманова // Системні дослідження та інформаційні технології. – 2008. - №3. – С. 52-65.

14. Хорошко В.А. Основи комп‘ютерної стеганографії: навчальний посібник для студентів і аспірантів / В.А.Хорошко, О.Д.Азаров, М.Є.Шелест, Ю.Є.Яремчук. — Вінниця: ВДТУ, 2003. -143 с.

15. Макконнелл Дж. Основы современных алгоритмов. 2-е дополненное издание / Дж. Макконнелл. — М.: Техносфера, 2004. — 368 с.

16. Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с.

17. Алиев, А.Т. Оценка стойкости систем скрытой передачи информации / А.Т. Алиев, А.В. Балакин // Известия ТРТУ. Тематический выпуск. Материалы VII Международной научно-практической конференции «Информационная безопасность». — Таганрог: Изд-во ТРТУ, 2005. — №4 (48). — С. 199–204.

18. Корольов, В.Ю. Планування досліджень методів стеганографії та стеганоаналізу / В.Ю. Корольов, В.В. Поліновський, В.А. Герасименко, М.Л. Горінштейн // Вісник Хмельницького національного університету. — 2011. — № 4. — С. 187–196.

19. Miller, A. Least Significant Bit Embeddings: Implementation and Detection [Электронный ресурс]: Computer Science Honors Thesis. – 2012. – Режим доступа: http://aaronmiller.in/thesis.

20. Chandramouli, R. Analysis of LSB based Image Steganography Techniques / R. Chandramouli, N. Memon // Proceedings of ICIP, Thessaloniki, Greece, October 7-10, 2001. — 2001. — Vol.3. — PP. 1019–1022.

21. Кобозева, А.А. Общий подход к анализу состояния информационных объектов, основанный на теории возмущений / А.А. Кобозева // Вісник Східноукраїнського національного університету ім. В. Даля. — 2008. — №8(126), Ч.1. — С. 72–81.

Лекция 8.ОБЕСПЕЧЕНИЕ НЕЧУВСТВИТЕЛЬНОСТИ СТЕГАНОСООБЩЕНИЯ К ВОЗМУЩАЮЩИМ ВОЗДЕЙСТВИЯМ

План

1. Введение.
2. Анализ возмущений сингулярных спектров цифровых изображений при различных возмущающих воздействиях

3. Анализ возмущений сингулярных векторов матриц (блоков матриц) цифровых изображений при разных возмущающих воздействиях.

Введение

Одно из основных требований, выдвигаемых к любому стеганографическому методу с целью обеспечения эффективного декодирования секретной информации – его устойчивость по отношению к возмущающим воздействиям: сгенерированное рассматриваемым методом СС должно быть нечувствительным (мало чувствительным) к возмущениям. При этом под чувствительностью стеганосообщения, как было сказано в лекции 5, будем понимать чувствительность задачи его построения.

Стегопреобразование контейнера, независимо от способа и области погружения дополнительной информации, можно представить в соответствии с (5.1) (лекция 5) как возмущение 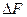исходной матрицы , а любое возмущающее воздействие, которое претерпевает СС в ходе транспортировки или хранения в виде дополнительного возмущающего воздействия с матрицей 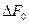или в виде совокупности возмущений полных наборов параметров (лекция 5), в качестве которых далее рассматриваются множества сингулярных чисел (СНЧ) и сингулярных векторов (СНВ) соответствующей матрицы СС.

Определим достаточные условия обеспечения нечувствительности СС к возмущающим воздействиям при формализации стеганопреобразования в виде возмущений СНЧ.