Алгоритм метода перемещений

2.1.1 Степень кинематической неопределимости

Главной характеристикой статически неопределимой конструкции, рассчитываемой методом перемещений, является степень кинематической неопределимости.

Степенью кинематической неопределимости называется число тех неизвестных перемещений, значения которых определяют деформированный вид стержневой системы и, следовательно, все усилия в ней.

Установим, какие перемещения стержня необходимо и достаточно знать, для того чтобы можно было определить внутренние усилия в любом его сечении. Для этого рассмотрим прямолинейный стержень АВ (рисунок 2.1), выделенный из n раз статически неопределимой рамы.

При представлении деформированного состояния рамы мы будем пренебрегать:

1) продольными деформациями стержней от продольных усилий N,

2) разницей длины искривленного стержня и проекцией его на первоначальное направление,

3) влиянием поперечных сил на деформацию изгиба стержня.

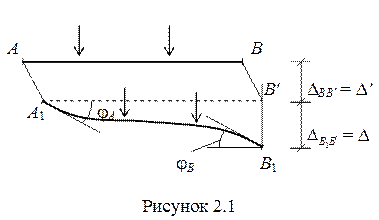
Под влиянием действующей на систему (в том числе и на сам стержень) нагрузки стержень перейдет в новое деформированное состояние А₁В₁. Переход стержня из положения АВ в положение А₁В₁ можно представить в виде суммы следующих перемещений.

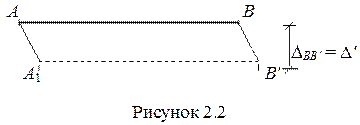
1) Поступательное перемещение из положения АВ в положение А В′ на величину Δ′. При этом в стержне не будет возникать внутренних усилий (рисунок 2.2).

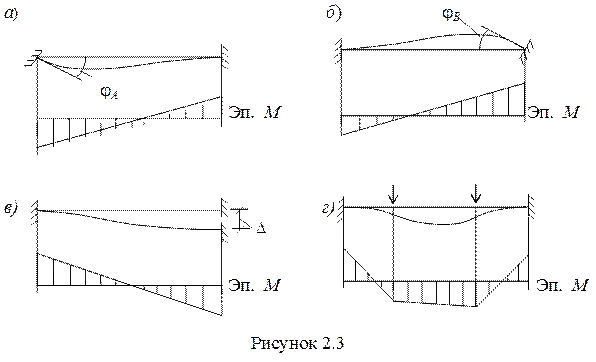
2) Поворот узла А на угол j_A. При этом в стержне будут возникать внутренние усилия в виде изгибающих моментов. На рисунке 2.3,а показаны изогнутая ось и эпюра изгибающих моментов, соответствующие такой деформации (слева у стержня растянуты нижние волокна, справа – верхние).

3) Поворот узла В на угол j_В. В стержне будут возникать изгибающие моменты, показанные на эпюре (рисунок 2.3,б).

4) Линейное смещение одного из концов стержня с защемленными краями на величину Δ (рисунок 2.3,в).

5) Перемещение точек оси стержня с защемленными краями от действия приложенных к стержню внешних сил (рисунок 2.3,г).

Складывая эпюры моментов от каждого воздействия, получим результирующую эпюру для рассматриваемого стержня. Другими словами, если мы знаем для нагруженного стержня значения перемещений его торцов j_A, j_A, D, то сможем определить внутренние усилия в любом сечении этого стержня.

Таким образом степень кинематической неопределимости n зависит от числа неизвестных улов поворота жестких узлов n_у и возможных линейных перемещений узлов n_л и равна сумме

n ₌n_{у +}n_л (2.1)

2.1.2 Основная система метода перемещений.

При расчете статически неопределимых систем методом перемещений стержневая система расчленяется на ряд однопролетных балок (стоек), которые чаще всего статически неопределимы. Это достигается введением в нее дополнительных связей, запрещающих линейные смещения и повороты узлов (На рис. 2.4 показано, что в жестком узле вводится заделка, а возможному линейному смещению препятствует введенная опора). В результате получается основная система метода перемещений.

Поскольку деформированное и силовое состояния эквивалентной системы не должно отличаться от напряженно-деформированного состояния заданной системы необходимо в эквивалентной системе ввести дополнительные перемещения z₁ и z₂, которые имеют место в заданной системе (рис. 2.4,а). Напомним, что под эквивалентной системой понимается основная система, нагруженная дополнительно заданной внешней нагрузкой и неизвестными..

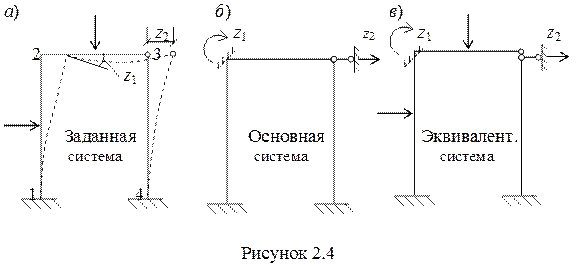
Вводимые в основной системе в жесткие узлы заделки называют плавающими, поскольку они отличаются от действительных жестких защемлений тем, что оказывают препятствие только повороту узла, но не препятствуют собственным линейным смещениям этого узла.

Если основная система метода сил получается путем отбрасывания лишних связей, то основная система метода перемещений получается путем добавления связей. При этом повышается степень статической неопределимости заданной системы.

Повторимся, что степень кинематической неопределимости определяется как сумма числа жестких узлов и числа возможных линейных смещений узлов.

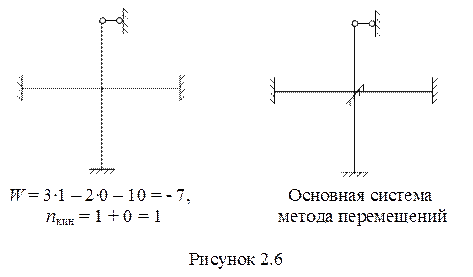
На рисунках 2.5, 2.6 и 2.7 показаны примеры выбора основной системы метода перемещений. Напомним, что W – степень статической неопределимости (число лишних связей)

.

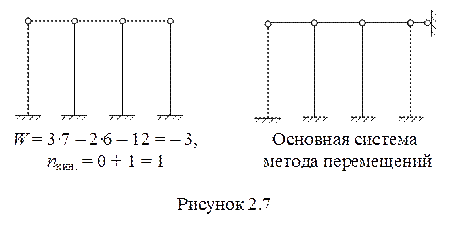
2.1.3 Канонические уравнения метода перемещений

Рассмотрим работу основной системы в методе перемещений и сравним с работой заданной системы (рисунок 2.8). В основной системе от действия внешней нагрузки в наложенных связях будут возникать реактивные усилия (реакции) R₁_P и R₂_P. Отметим, что суммарная реакция R₁_P (на рисунке не показана)равна R′₁_P + R′′₁_P, поскольку в левом жестком узле расположен верхний конец левой стойки, момент в котором равен R′₁_P и левый конец ригеля с моментом R′′₁_P .

В заданной системе этих реакций нет. Реактивные моменты и силы можно обратить в нуль, если повернуть заделку на угол, равный действительному углу поворота z₁ и сместить узлы ригеля так, чтобы их смещение равнялось действительному смещению z₂.

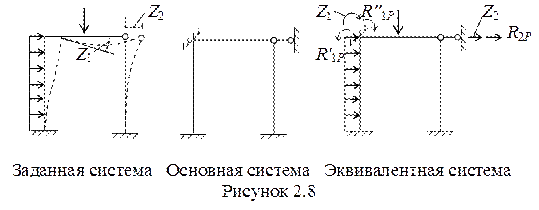
Отрицание реактивных усилий в веденных связях лежит в основе канонических уравнений метода перемещений. Коротко эти уравнения можно записать так: SR₁_i = 0, SR₂_i = 0, … SR_ni = 0 – сумма реакций в каждой наложенной связи равна нулю.

Рассмотрим подробно в развернутом виде для нашего примера первое уравнение

SR₁_i = R_1Р + R₁₁ + R₁₂ = 0, (а)

где: R_1Р – реакции в первой введенной связи от внешней нагрузки, R₁₁ – реакции в первой введенной связи от первого перемещения z₁, R₁₂ – реакции в первой введенной связи от от второго перемещения z₂ .

Реакции от перемещений можно представить в таком виде:

R₁₁ = Z₁∙r₁₁, R₁₂ = Z₂∙r_12.

где: Z₁, Z₂ – искомые перемещения узлов, r₁₁, r₁₂– реакции в наложенных связях от единичных смещений этих связей (рисунок 2.9).

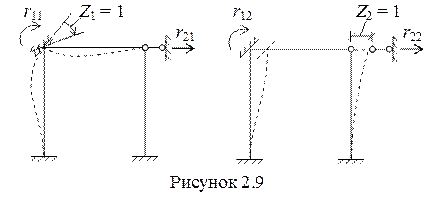
Тогда уравнение (а) примет вид

Z₁∙r₁₁+Z₂∙r₁₂ + R_1Р = 0,

аналогично для второй связи

Z₁∙r₂₁+ Z₂∙r₂₂ + R_2Р = 0.

В общем виде система канонических уравнений метода перемещений имеет вид:

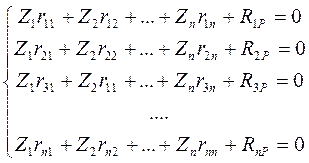(2.4)

где – r₁₁, r₂₂, ... r_ii … r_nn - главные коэффициенты,

– r₁₂, r₂₁, r₁₃, r₂₃ … r_ij - побочные коэффициенты. В соответствии с теоремой о взаимности реакций выполняется условие: r_ij = r_ji,

– R_1Р, R_2Р,…R_n_Р – грузовые реакции (свободные члены системы алгебраических уравнений (2.4)).

Физический смысл канонических уравнений (2.4) заключается в следующем – сумма реакций в каждой наложенной связи от действия внешней нагрузки и от угловых и линейных смещений равна нулю.

2.1.4 Определение коэффициентов и свободных членов канонических уравнений

Для определения коэффициентов и свободных членов канонических уравнений необходимо в основной системе построить эпюры моментов от нагрузки и от единичных смещений наложенных связей. Построение эпюр изгибающих моментов производится при помощи таблиц (см. приложение В). В таблицах приводятся эпюры моментов для статически неопределимых балок, полученные методом сил.

Значения коэффициентов и свободных членов уравнений (2.4) получаем из рассмотрения равновесия узлов рамы в единичных и грузовом состояниях (по единичным и грузовой эпюрам). Порядок определения коэффициентов и свободных членов канонических уравнений покажем на примере.

<91011 12 13 14 15 >

Дата добавления: 2017-02-13; просмотров: 4994;