Примеры использования нового метода

Рассмотрим хорошо известный СМ замены наименьшего значащего бита (LSB). Процесс стеганопреобразования будем трактовать как аддитивное погружение ДИ в пространственной области в соответствии с (5.1). Заметим, что 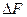в общем случае не является непосредственно матрицей секретного сообщения, но она однозначно строится по заданой ДИ. В данном конкретном примере, если значение очередного бита, который встраивается в контейнер, совпадает со значением LSB текущего пикселя ОС, то соответствующее значение элемента 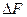будет равно 0, иначе элемент 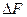принимает значения +1 или -1. 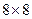Для наглядной иллюстрации использования предложенного метода рассмотрим как ОС матрицу размера (рис.6.1(а)), которая отвечает блоку, расположенному на пересечении первой блочной строки и третьего блочного столбца изображения POUT.TIF после его стандартного разбиения. Матрице общего вида поставим в соответствие симметричные матрицы 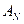, 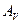по формуле (5.2) (рис.1(б,в)). Пусть 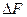отвечает ДИ, которая встраивается в блок , сформованная случайным образом, имеет вид, представленный на рис.6.2(а), 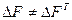. Разобьем 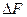на две части: нижний треугольник 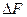после симметричного отражения относительно главной диагонали отвечает той части секретного сообщения ( 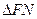(рис.6.3(б))), которая будет встраиваться в 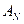; верхний треугольник после аналогичной трансформации ( 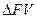) - информация, которая встраивается в 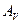. Дальше для простоты изложения будем рассматривать только одну матрицу, например, 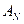, называя ее матрицей ОС.

Для сохраннения симметричности используемых для обработки матриц процесс построения блока СС 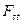распадается на два этапа: а) 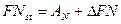, б) 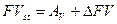, блок СС получается как объединение нижнего треугольника 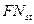і верхнего треугольника .

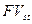Рис.6.1. а – матрица блока ОС; б,в - симметричные матрицы, которые отвечают блоку F ОС.

Рис.6.2. Матрица ДИ: а – которая отвечает блоку F; б - которая отвечает блоку A _N; в - которая отвечает блоку A_V.

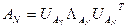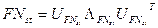Построим нормальные СР: и , результаты которых представлены на рис.6.3. Стеганопреобразование незначительно возмутило спектр и СВ, которые отвечают 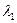,..., , 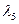а сравнительно большие возмущения получили СВ, отвечающие наименьшим по модулю СЗ 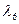, , 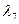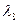с наименьшей абсолютной отделенностью (на рис.6.3 жирным шрифтом). Таким образом, рассмотренное стеганопреобразование обеспечивает надежность восприятия СС после встраивания ДИ, но полученное СС будет чувствительным к возмущающим воздействиям.

Выводы, сделанные на основе теоретических выкладок, полностью отвечают известным характеристикам метода LSB.

Рассмотрим пример использования предложенного подхода для сравнения параметров нескольких СМ. Пусть случайно сформированное бинарное сообщение погружается аддитивно в ОС а) в контур; б) произвольно. Как ОС рассмотрим блок изображения POUT, матрица которого представлена на рис.6.1(а). Этот блок содержит часть контура. Для определенности рассмотрим матрицу, которая отвечает верхнему треугольнику F - A_V. На рис.6.4(а) представлены результаты встраивания ДИ случайним образом, а на рис.6.4(б) встраивание происходило в контур, .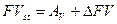

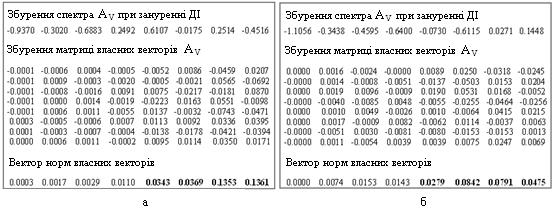
Рис.6.4. а - результат встраивания ДИ произвольным образом; б - результат встраивания ДИ в контур ОС

Сравнивая возмущения матриц СВ, можно увидеть, что возмущение при встраивании вне контура "зацепят" и СВ, для которого СЗ имеет наибольшую абсолютную отделенность, в то время, как при встраивании в контур такого не происходит. Это означает, что надежность восприятия СС будет лучшей при встраивании в контур (это хорошо известный факт), чувствительность СС к возмущающим воздействиям в обоих методах большая (наибольшие возмущения получили СВ, которые отвечают СЗ с малой абсолютной отделенностью) и почти одинаковая, что также отвечает известным характеристикам сравниваемых алгоритмов встраивания ДИ.

Таким образом, рассмотренный подход дает возможность формализовать процесс качественного сравнения СМ, независимо от их конкретного вида и используемой области встраивания ДИ.

Вопросы

1. Каким образом для блоков матрицы произвольного цифрового изображения строится нормальное спектральное разложение с вещественными собственными значениями?

2. Чем обусловлена единственность нормального спектрального разложения матрицы?

3. Как оценивается возмущение собственных векторов блоков матрицы контейнера при стеганопреобразовании?

4. Какие свойства стеганографического алгоритма рассматриваются как основные?

5. Как происходит сравнение основных свойств нескольких стеганографических алгоритмов?

6. Вычислительные затраты метода сравнения свойств стеганографических алгоритмов? Можно ли эти затраты уменьшить? Ответ обосновать.

7. Формальная оценка свойств метода модификации наименьшего значащего бита при разных выборах стеганопути.

Литература

1. Кобозєва А.А. Аналіз захищеності інформаційних систем / Кобозєва А.А., Хорошко В.А., Мачалін І.О. – К.: Вид.ДУІКТ, 2010. – 316 с.

2. Кобозева А.А. Анализ информационной безопасности / А.А.Кобозева, В.А.Хорошко. – К.: Изд. ГУИКТ, 2009. – 251 с.

3. Деммель Дж. Вычислительная линейная алгебра / Дж.Деммель; пер.с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 430 с.

4. Бахвалов Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. — М.: БИНОМ. Лаборатория знаний, 2006. — 636 с.

5. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.

6. Гантмахер Ф.Р. Теория матриц / Ф.Р.Гантмахер. — М.: Наука, 1988. — 552 с.

7. Грибунин В.Г. Цифровая стеганография / В.Г.Грибунин, И.Н.Оков, И.В.Туринцев. — М.: Солон-Пресс, 2002. — 272с.

8. Стеганография, цифровые водяные знаки и стеганоанализ : [монография] / А.В. Аграновский, А.В. Балакин, В.Г. Грибунин, С.А. Сапожников. — М.: Вузовская книга, 2009. — 220 с.

9. Кобозева А.А. Применение сингулярного и спектрального разложения матриц в стеганографических алгоритмах / А.А.Кобозева // Вісник Східноукр-го нац-го ун-ту ім. В.Даля. — 2006. — №9(103), ч.1. — С.74—82.

10. Конахович Г.Ф. Компьютерная стеганография. Теория и практика / Г.Ф.Конахович, А.Ю.Пузыренко. — К.: МК — Пресс, 2006. — 288 с.

11. Кобозева А.А. Учет свойств нормального спектрального разложения матрицы контейнера при обеспечении надежности восприятия стегосообщения / А.А.Кобозева, Е.А.Трифонова // Вестник НТУ «ХПИ». — 2007. — №18. — С.81—93.

12. Кобозева А.А. Оценка чувствительности стегосообщения к возмущающим воздействиям / А.А.Кобозева, Е.В.Нариманова // Системні дослідження та інформаційні технології. – 2008. - №3. – С. 52-65.

13. Хорошко В.А. Основи комп‘ютерної стеганографії: навчальний посібник для студентів і аспірантів / В.А.Хорошко, О.Д.Азаров, М.Є.Шелест, Ю.Є.Яремчук. — Вінниця: ВДТУ, 2003. -143 с.

14. Воеводин В.В. Вычислительные основы линейной алгебры / В.В.Воеводин. — М.: Наука. Гл.ред.физ.-мат.лит., 1977. — 304 с.

15. Алиев, А.Т. Оценка стойкости систем скрытой передачи информации / А.Т. Алиев, А.В. Балакин // Известия ТРТУ. Тематический выпуск. Материалы VII Международной научно-практической конференции «Информационная безопасность». — Таганрог: Изд-во ТРТУ, 2005. — №4 (48). — С. 199–204.

16. Корольов, В.Ю. Планування досліджень методів стеганографії та стеганоаналізу / В.Ю. Корольов, В.В. Поліновський, В.А. Герасименко, М.Л. Горінштейн // Вісник Хмельницького національного університету. — 2011. — № 4. — С. 187–196.

17. Miller, A. Least Significant Bit Embeddings: Implementation and Detection [Электронный ресурс]: Computer Science Honors Thesis. – 2012. – Режим доступа: http://aaronmiller.in/thesis.

18. Chandramouli, R. Analysis of LSB based Image Steganography Techniques / R. Chandramouli, N. Memon // Proceedings of ICIP, Thessaloniki, Greece, October 7-10, 2001. — 2001. — Vol.3. — PP. 1019–1022.

19. Кобозева, А.А. Общий подход к анализу состояния информационных объектов, основанный на теории возмущений / А.А. Кобозева // Вісник Східноукраїнського національного університету ім. В. Даля. — 2008. — №8(126), Ч.1. — С. 72–81.

Лекция 7. Метод повышения устойчивости стеганографических алгоритмов

1. Способ пересылки и декодирования дополнительной информации.

2. Условия устойчивости метода SYSTEMA.

3. Способ обеспечения малого числа обусловленности Скила матрицы произвольного изображения.

4.Практическая реализация метода SYSTEMA.

1. Способ пересылки и декодирования дополнительной информации

Пусть — 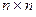-матрица ОС, 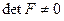, а в качестве ДИ выступает случайно сформированная бинарная числовая последовательность, содержащая 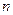элементов из множества 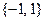, рассматриваемая ниже как вектор 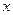длины 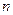. Последовательность может содержать менее 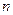элементов, тогда она дополняется незначащими элементами до нужной длины.

Основные шаги метода двухэтапного декодирования ДИ SYSTEMA следующие:

1. Погружение ДИ.

а) Вычислить произведение

.

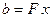В предположении отсутствия ошибок округления, вектор 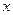является

точным решением СЛАУ

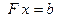. (7.1)

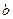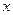б) Вектор погрузить в вместо вектора ДИ каким- либо СМ (СМ1).

1. Декодирование .

а) Из полученого СС, возможно подвергшегося возмущениям при пересылке, извлечь погруженный вектор 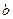в возмущенном виде 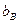при помощи СМ1. После извлечения вектора 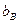матрица изображения 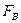, в общем случае, будет отлична от .

б) Извлечь 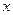путем решения неоднородной СЛАУ

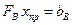, (7.2)

где ;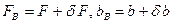

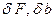— возмущения матрицы системы и вектора правой части 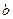соответственно;

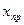— результат декодирования 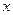в условиях возмущенных входных данных.

Использование предлагаемого способа пересылки и декодирования ДИ SYSTEMA, включающего дополнительный этап в виде решения СЛАУ, при обеспечении достаточного условия устойчивости метода, обоснованного ниже, дает возможность увеличить объем 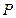правильно восстановленной информации по сравнению с непосредственной пересылкой 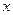на месте вектора 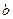при абсолютно аналогичных условиях.

2. Условие устойчивости метода SYSTEMA

Пусть 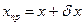, где 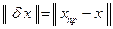— абсолютная погрешность 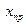. Тогда СЛАУ (7.2) представляется в виде:

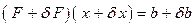(7.3)

Учитывая, что 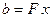и 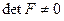, выразим из (7.3) :

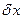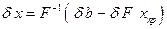, (7.4)

откуда, принимая во внимание элементарные свойства нормы и невырожденность матрицы , получаем:

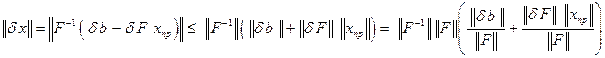. (7.5)

Выбор конкретных матричной и векторной норм не существенен, поэтому никак не оговаривается. Важно лишь, что эти нормы согласованные.

Поскольку 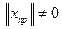, разделив неравенство (7.5) на 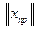, получим:

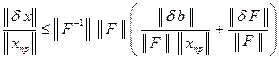. (7.6)

Из (7.6) вытекает, что 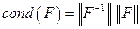является числом обусловленности, а значит мерой чувствительности задачи о решении СЛАУ к погрешности в исходных данных. Если число обусловленности матрицы ОС мало, задача декодирования ДИ на втором этапе SYSTEMA является нечувствительной, малые возмущения на входе незначительно изменят результат, .

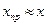Предположим, что значения

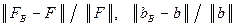(7.7)

невелики. Соотношения (7.7) анализируют возмущения всей матрицы и всего вектора в целом. Даже большая погрешность, возникающая в отдельных пикселях СС при небольшом их количестве не отразится значительно на оценках для выражений (7.7), а, значит, при хорошей обусловленности матрицы , и на значениях элементов вектора 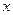в силу (7.6), хотя некоторые элементы 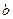могут быть сильно «испорчены». Подтверждением этого являются результаты вычислительного эксперимента, приведенные ниже.

Основным вычислительным звеном SYSTEMA является решение СЛАУ (7.2). Применение устойчивого численного метода к произвольной неоднородной системе с невырожденной матрицей в общем случае не гарантирует получение результата с малой погрешностью. Даже если вектор невязки, определяемый как

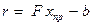, (7.8)

мал, это не означает, что 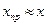. Действительно, из (7.8) получаем, что 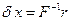, и соответственно

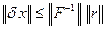, (7.9)

откуда 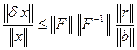. Очевидно, что малость (7.8) гарантирует малую относительную погрешность решения только в том случае, когда матрица системы хорошо обусловлена.

Таким образом, для эффективного использования метода SYSTEMA в качестве контейнера нужно использовать ЦИ, с хорошо обусловленной матрицей.

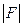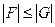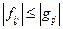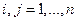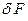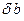Заметим, что на практике оценка (7.6) часто оказывается завышенной. Пусть — матрица, составленная из модулей элементов , а неравенство типа понимается как система покомпонентных неравенств для элементов матриц: для всех . Аналогичные обозначения используются и для векторов. На практике часто можно добиться того, чтобы и удовлетворяли оценкам :

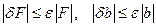(7.10)

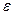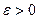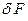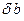где — некоторое очень малое число — относительная погрешность входных данных. Наименьшее число , для которого существуют возмущения и , удовлетворяющие оценкам (7.10) и уравнению (7.3), выражается через невязку 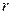, определяемую соотношением (7.8), формулой:

.

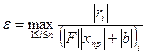Из (7.4) получаем:

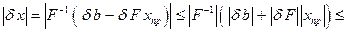
(7.11)

.

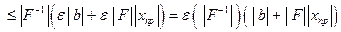Предположим, что используемая векторная норма обладает свойством: 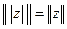, (такими будут, например, max-норма, евклидова норма), тогда из (7.11) получаем:

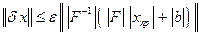. (7.12)

Если возмущению подверглась только матрица системы , а вектор правой части остался неизменным ( 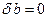), тогда из (7.11) вытекает оценка, подобная (7.12), имеющая вид: 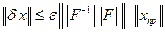, а для относительной погрешности полученного 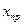имеем:

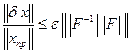. (7.13)

Величина 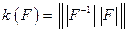— число обусловленности Скила — также, как и 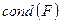, позволяет оценить относительную погрешность результата через относительную погрешность входных данных 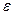, может использоваться для оценки погрешности результата и в случае, если 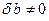. Действительно, из (7.12) получаем:

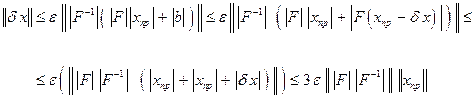
Откуда 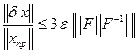. Имеет место также оценка, аналогичная (7.9):

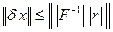(7.14)

На практике оценки (7.13) и (7.14) могут быть значительно меньше аналогичных оценок (7.6) и (7.9). Это приводит к тому, что СЛАУ даже с большим 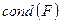может решаться с высокой точностью.

Из оценок (7.13) - (7.14) и предположения об устойчивости СМ1, используемого для декодирования вектора 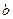, вытекает истинность следующей теоремы.

Теорема. Пусть матрица изображения, используемого в качестве ОС, имеет малое число обусловленности Скила. Тогда метод SYSTEMA является устойчивым.