Способ обеспечения малого числа обусловленности Скила матрицы произвольного изображения
Оценка числа обусловленности Скила для матрицы ОС является ключевым моментом в вопросе выбора подходящего для пересылки ДИ методом SYSTEMA контейнера. Непосредственное вычисление числа обусловленности Скила для матриц большой размерности — процесс дорогостоящий. Кроме того, если контейнер является навязанным, его матрица плохо обусловлена, это, на первый взгляд, вообще лишает возможности использование метода SYSTEMA для обеспечения дополнительной защиты секретной информации.
Предлагается способ, позволяющий использовать практически любое изображение в качестве ОС в методе SYSTEMA, независимо от его реального числа обусловленности.
Для диагональной матрицы 
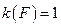 , а значит SYSTEMA будет устойчив. Аналогичную картину можно ожидать и в случае, когда для элементов
, а значит SYSTEMA будет устойчив. Аналогичную картину можно ожидать и в случае, когда для элементов  выполняется условие:
выполняется условие:
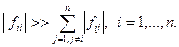 (7.15)
(7.15)
Но реальные изображения редко удовлетворяют свойству (7.15). Обеспечим малость числа обусловленности Скила матрицы изображения, не изменяя ее явно, а лишь моделируя виртуально значительное диагональное преобладание.
Пусть 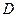 — диагональная матрица размером
— диагональная матрица размером 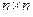 с элементами
с элементами 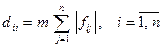 , где
, где 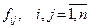 , — элементы матрицы
, — элементы матрицы  исходного изображения,
исходного изображения, 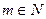 — параметр. Выбор
— параметр. Выбор 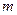 обеспечивает для
обеспечивает для 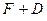 наличие свойств, близких к (7.15), но поскольку
наличие свойств, близких к (7.15), но поскольку 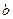 для используемой СЛАУ вычисляется в соответствии с выражением
для используемой СЛАУ вычисляется в соответствии с выражением 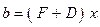 , то значение
, то значение 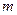 не может быть произвольно большим.
не может быть произвольно большим.
Реально матрица  не меняется, а виртуально построенная для нее матрица
не меняется, а виртуально построенная для нее матрица 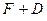 очевидно имеет диагональное преобладание. При получении СС, для которого ОС — матрица
очевидно имеет диагональное преобладание. При получении СС, для которого ОС — матрица 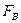 , на втором этапе декодирования в SYSTEMA решается СЛАУ
, на втором этапе декодирования в SYSTEMA решается СЛАУ
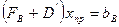 , (7.16)
, (7.16)
где 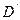 — диагональная матрица, которая формируется декодером по полученной возмущенной матрице
— диагональная матрица, которая формируется декодером по полученной возмущенной матрице 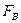 с элементами
с элементами 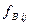 :
: 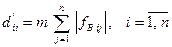 ,
, 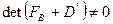 .
.
Поскольку свойства матрицы системы (7.16) близки к свойствам (7.15), решение СЛАУ (7.16) 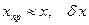 мало. Таким образом, практический метод введения виртуальной диагонали в матрицу реального изображения обеспечивает хорошую обусловленность Скила матрицы СЛАУ для декодирования ДИ и устойчивость SYSTEMA практически для любого ОС в предположении устойчивости алгоритма СМ1 декодирования b.
мало. Таким образом, практический метод введения виртуальной диагонали в матрицу реального изображения обеспечивает хорошую обусловленность Скила матрицы СЛАУ для декодирования ДИ и устойчивость SYSTEMA практически для любого ОС в предположении устойчивости алгоритма СМ1 декодирования b.
Дата добавления: 2016-07-22; просмотров: 1833;











