Алгоритм метода простых итераций

1.Преобразуем систему к нормальному виду: 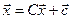, 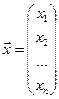– вектор неизвестных х₁, х₂, …, х_n, 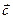- вектор свободных членов. (Выразим из первого уравнения х₁, из второго – х₂ и т.д.)

2. Выбираем начальное приближение – произвольный вектор 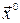, чаще всего нулевой (поэтому и называется нулевым приближением).

3. Строим итерационную последовательность по формуле: 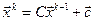, где k =0,1, ... Условие окончания: процесс продолжается до тех пор, пока 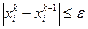, ε – заданная точность.

Теорема.Система линейных алгебраических уравнений имеет единственное решение, то есть итерации сходятся к решению со скоростью геометрической прогрессии независимо от выбора начального приближения, если норма матрицы С меньше единицы: .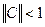

Норма матрицы определяется тремя способами:

1) 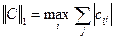- максимальная сумма модулей элементов матрицы по строкам,

2) 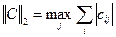- максимальная сумма модулей элементов матрицы по столбцам,

3) 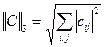корень квадратный из суммы квадратов модулей всех элементов матрицы.

Пример.Найти решение системы 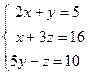с помощью метода итераций с точностью до ε = 0,5.

Решение.

1) Преобразуем систему к нормальному виду (поменяем местами второе и третье уравнения): 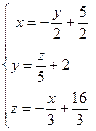. Матрица 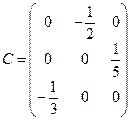, векторы 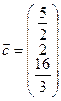и .

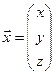2) Проверим, можно ли найти решение данным методом, то есть сойдутся ли итерации к решению. Для этого найдем норму матрицы С (например, первую):

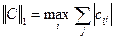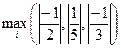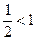= = , следовательно, итерации сходятся к решению.

3) Выберем в качестве начального приближения нулевой вектор: .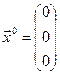

4) Найдем первую итерацию: 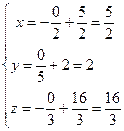, тогда первая итерация равна .

Проверим условие окончания 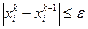, то есть 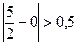, , 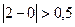, 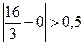следовательно, итерационный процесс следует продолжить. (Достаточно было проверить только первое неравенство).

5) Найдем вторую итерацию: 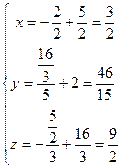, тогда вторая итерация равна .

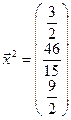Проверим условие 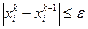, то есть 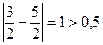, следовательно, итерационный процесс следует продолжить.

6) Найдем третью итерацию: 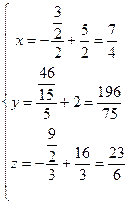, тогда третья итерация равна .

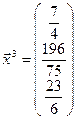Проверим условие 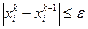, то есть 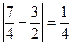< 0,5 - истинно, 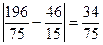< 0,5 – истинно, 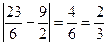> 0,5, следовательно, итерационный процесс следует продолжить.

7) Найдем четвертую итерацию: 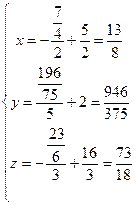, четвертая итерация равна .

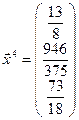Проверим условие 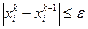, то есть 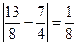< 0,5 - истинно, 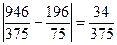< 0,5 – истинно, 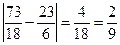< 0,5 - истинно, следовательно, итерационный процесс закончен, найдено приближенное решение системы 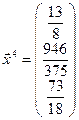с точностью до ε = 0,5.

Ответ: 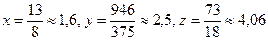. (Точное решение (1, 3, 5)).

Замечание. Систему линейных уравнений можно привести к нормальному виду также следующим образом: записать коэффициенты при неизвестных х₁, х₂, …, х_n в соответствующих уравнениях системы в виде kх, где k – число, близкое к коэффициенту при соответствующем неизвестном и на которое можно легко разделить коэффициенты при неизвестных и свободные члены. Обычно k = 10.

Пример. Привести систему 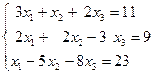к нормальному виду.

Решение.

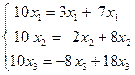, отсюда , ,

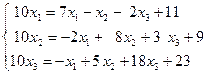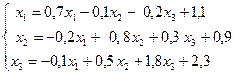где матрица 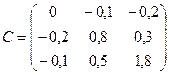, векторы 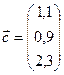и .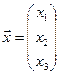

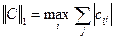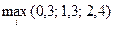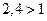= = , следовательно, метод итераций расходится. Данным методом систему уравнений не решить.

Замечание.Существуют формулы для подсчета числа итераций.