Сингулярные векторы блоков матриц изображений, отвечающие максимальным сингулярным числам, при разном качестве сжатия
| Формат ЦИ | Сингулярный вектор |
JPEG ( 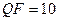 ) )
|  : 0.3536 0.3536 0.3536 0.3535 0.3535 0.3535 0.3536 0.3536 : 0.3536 0.3536 0.3536 0.3535 0.3535 0.3535 0.3536 0.3536
|
 : 0.3541 0.3538 0.3533 0.3531 0.3531 0.3533 0.3538 0.3541 : 0.3541 0.3538 0.3533 0.3531 0.3531 0.3533 0.3538 0.3541
| |
JPEG ( 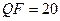 ) )
|  : 0.3780 0.3747 0.3681 0.3581 0.3481 0.3381 0.3314 0.3281 : 0.3780 0.3747 0.3681 0.3581 0.3481 0.3381 0.3314 0.3281
|
 : 0.3667 0.3634 0.3601 0.3568 0.3501 0.3468 0.3435 0.3401 : 0.3667 0.3634 0.3601 0.3568 0.3501 0.3468 0.3435 0.3401
| |
JPEG ( 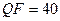 ) )
|  : 0.3898 0.4007 0.4079 0.3960 0.3679 0.3193 0.2678 0.2351 : 0.3898 0.4007 0.4079 0.3960 0.3679 0.3193 0.2678 0.2351
|
 : 0.2370 0.1812 0.1695 0.2714 0.3965 0.4957 0.4691 0.4309 : 0.2370 0.1812 0.1695 0.2714 0.3965 0.4957 0.4691 0.4309
| |
JPEG ( 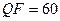 ) )
|  : 0.3107 0.3273 0.3497 0.3656 0.3701 0.3675 0.3659 0.3667 : 0.3107 0.3273 0.3497 0.3656 0.3701 0.3675 0.3659 0.3667
|
 : 0.4020 0.3885 0.3673 0.3462 0.3318 0.3265 0.3273 0.3299 : 0.4020 0.3885 0.3673 0.3462 0.3318 0.3265 0.3273 0.3299
| |
JPEG ( 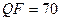 ) )
|  : 0.2438 0.2435 0.2574 0.3268 0.3926 0.4206 0.4375 0.4310 : 0.2438 0.2435 0.2574 0.3268 0.3926 0.4206 0.4375 0.4310
|
 : 0.3482 0.3504 0.3539 0.3566 0.3570 0.3561 0.3537 0.3525 : 0.3482 0.3504 0.3539 0.3566 0.3570 0.3561 0.3537 0.3525
| |
JPEG ( 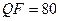 ) )
|  : 0.3542 0.3506 0.3499 0.3521 0.3534 0.3528 0.3556 0.3598 : 0.3542 0.3506 0.3499 0.3521 0.3534 0.3528 0.3556 0.3598
|
 : 0.3485 0.3427 0.3544 0.3468 0.3570 0.3568 0.3599 0.3618 : 0.3485 0.3427 0.3544 0.3468 0.3570 0.3568 0.3599 0.3618
| |
JPEG ( 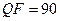 ) )
|  : 0.3416 0.3487 0.3585 0.3620 0.3562 0.3487 0.3528 0.3595 : 0.3416 0.3487 0.3585 0.3620 0.3562 0.3487 0.3528 0.3595
|
 : 0.3409 0.3448 0.3452 0.3519 0.3484 0.3525 0.3708 0.3724 : 0.3409 0.3448 0.3452 0.3519 0.3484 0.3525 0.3708 0.3724
| |
JPEG ( 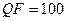 ) )
|  : 0.4059 0.3903 0.3917 0.3908 0.3880 0.3545 0.2663 0.1718 : 0.4059 0.3903 0.3917 0.3908 0.3880 0.3545 0.2663 0.1718
|
 : 0.2991 0.2064 0.2047 0.3272 0.4022 0.4039 0.4614 0.4256 : 0.2991 0.2064 0.2047 0.3272 0.4022 0.4039 0.4614 0.4256
| |
| TIF |  : 0.3527 0.3513 0.3512 0.3534 0.3535 0.3525 0.3558 0.3580 : 0.3527 0.3513 0.3512 0.3534 0.3535 0.3525 0.3558 0.3580
|
 : 0.3462 0.3462 0.3517 0.3505 0.3553 0.3587 0.3589 0.3606 : 0.3462 0.3462 0.3517 0.3505 0.3553 0.3587 0.3589 0.3606
|
Из всего вышесказанного вытекает, что малым при сжатии будет не только отклонение сингулярных векторов  и
и  от первоначального положения, что говорит о «классической» нечувствительности данных векторов, но и изменение во взаимном расположении
от первоначального положения, что говорит о «классической» нечувствительности данных векторов, но и изменение во взаимном расположении  ,
,  , n-оптимального вектора.
, n-оптимального вектора.
Для комплексной количественной оценки полученного качественного заключения был проведен вычислительный эксперимент, в котором анализировались значения углов между векторами  и n-оптимальным,
и n-оптимальным,  и n-оптимальным,
и n-оптимальным,  и
и  для цифровых изображений, первоначально хранимых в формате без потерь, а затем после сжатия с различными коэффициентами качества
для цифровых изображений, первоначально хранимых в формате без потерь, а затем после сжатия с различными коэффициентами качества 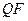 . Иллюстрация типичных результатов представлена для одного из тестируемых ЦИ на рис.8.4-8.6.
. Иллюстрация типичных результатов представлена для одного из тестируемых ЦИ на рис.8.4-8.6.
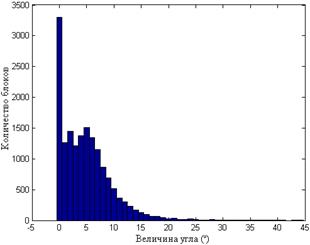
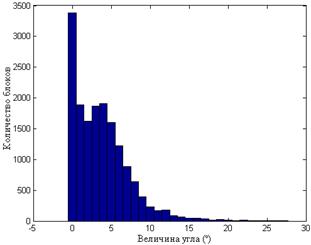
Из представленных гистограмм видно, что качественная картина взаимного расположения векторов  ,
,  , n-оптимального практически не зависит от коэффициента качества при сжатии, в частности, глобальный максимум всех гистограмм для рассматриваемого цифрового изображения наблюдается в нуле. При этом средние значения для углов между сингулярными векторами
, n-оптимального практически не зависит от коэффициента качества при сжатии, в частности, глобальный максимум всех гистограмм для рассматриваемого цифрового изображения наблюдается в нуле. При этом средние значения для углов между сингулярными векторами  и
и  ,
,  и n-оптимальным,
и n-оптимальным,  и n-оптимальным по всему изображению соответственно составили:
и n-оптимальным по всему изображению соответственно составили:
для TIF-ЦИ — 5.0, 3.7, 3.2;
для JPEG-ЦИ ( 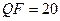 ) – 4.8, 3.6, 3.0;
) – 4.8, 3.6, 3.0;
для JPEG-ЦИ ( 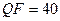 ) — 4.9, 3.7, 3.1;
) — 4.9, 3.7, 3.1;
для JPEG-ЦИ ( 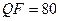 ) — 4.9, 3.7, 3.2,
) — 4.9, 3.7, 3.2,
т.е. взаимное расположение векторов  ,
,  , n-оптимального для рассмотренного примера практически не изменяется при различных по силе возмущающих воздействиях, отвечающих сжатию.
, n-оптимального для рассмотренного примера практически не изменяется при различных по силе возмущающих воздействиях, отвечающих сжатию.
а б
в г
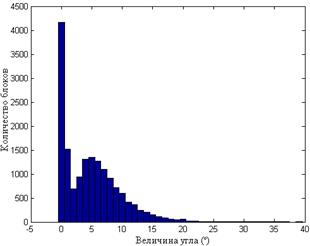
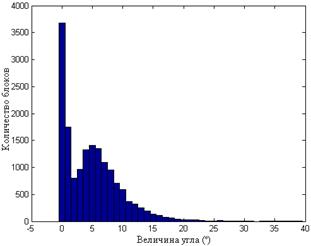
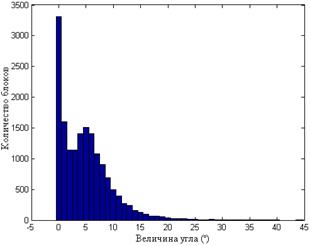
Рис.8.4. Гистограммы значений углов между СНВ  и
и  блоков для одного ЦИ при различных форматах хранения: TIF (а); JPEG
блоков для одного ЦИ при различных форматах хранения: TIF (а); JPEG 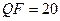 (б); JPEG
(б); JPEG 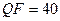 (в); JPEG
(в); JPEG 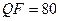 (г)
(г)
В ходе эксперимента для каждого ЦИ в формате TIF, а затем после пересохранения его в JPEG с различными значениями коэффициента качества 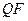 вычислялись средние значения углов между
вычислялись средние значения углов между  и
и  (обозначаемое как
(обозначаемое как 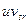 ),
),  и n-оптимальным (
и n-оптимальным ( 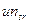 ),
),  и n-оптимальным (
и n-оптимальным ( 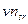 ) по всему изображению.
) по всему изображению.
а б
в г
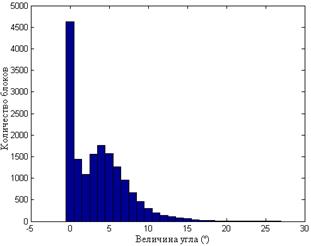
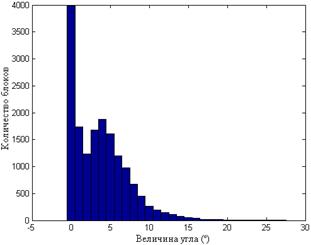
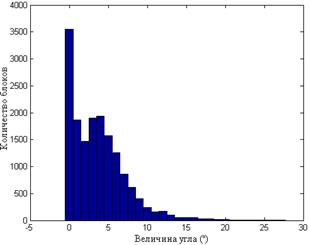
Рис.8.5. Гистограммы значений углов между СНВ блоков  и n-оптимальным для одного ЦИ при различных форматах хранения: TIF (а); JPEG
и n-оптимальным для одного ЦИ при различных форматах хранения: TIF (а); JPEG 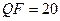 (б); JPEG
(б); JPEG 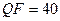 (в); JPEG
(в); JPEG 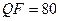 (г)
(г)
Для 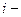 го ЦИ эти значения обозначались соответственно
го ЦИ эти значения обозначались соответственно 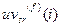 ,
, 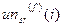 ,
, 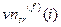 ,
, 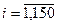 , где верхний индекс
, где верхний индекс 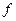 указывает на формат хранения ЦИ (для JPEG-ЦИ он указывает на значение коэффициента качества
указывает на формат хранения ЦИ (для JPEG-ЦИ он указывает на значение коэффициента качества  , использованного при сжатии).
, использованного при сжатии).
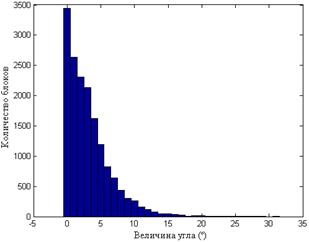
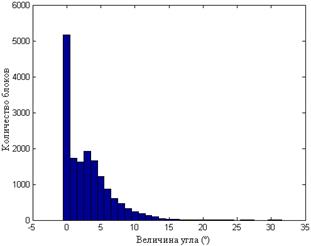
а б
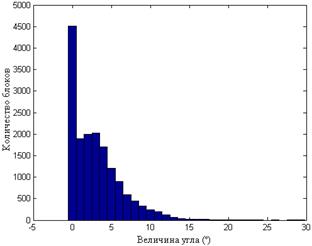
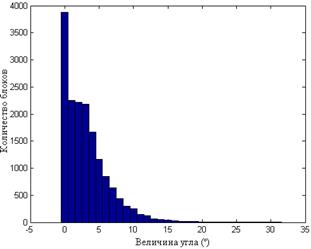
в г
Рис.8.6. Гистограммы значений углов между СНВ блоков  и n-оптимальным для одного ЦИ при различных форматах хранения: TIF (а); JPEG
и n-оптимальным для одного ЦИ при различных форматах хранения: TIF (а); JPEG 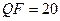 (б); JPEG
(б); JPEG 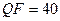 (в); JPEG
(в); JPEG 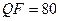 (г)
(г)
Результаты проведенного вычислительного эксперимента для наибольшего из рассмотренных возмущающих воздействий ( 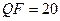 ) отражены на рис.8.7, в табл.8.4, откуда видно, что для подавляющего большинства изображений
) отражены на рис.8.7, в табл.8.4, откуда видно, что для подавляющего большинства изображений 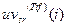 ,
, 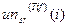 ,
, 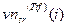 претерпевают при сжатии с
претерпевают при сжатии с 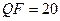 возмущение, не превосходящее одного градуса (рис.8.7), при этом средние значения
возмущение, не превосходящее одного градуса (рис.8.7), при этом средние значения 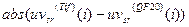 ,
, 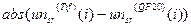 ,
, 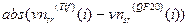 ,
, 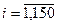 , соответственно равны 0.58, 0.45, 0.41.
, соответственно равны 0.58, 0.45, 0.41.
а б
в
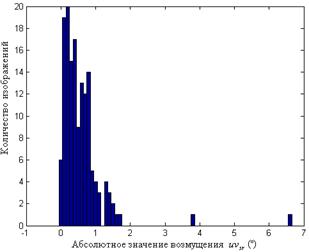
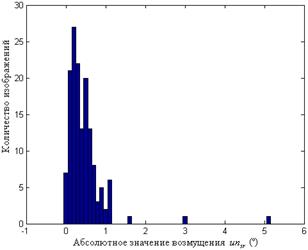
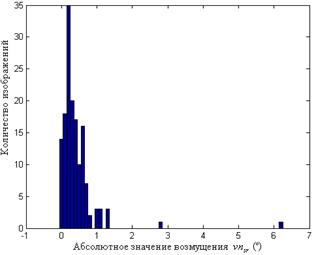
Рис.8.7. Результат сжатия ЦИ, хранящегося первоначально без потерь: гистограмма значений 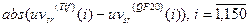 (а); гистограмма значений
(а); гистограмма значений 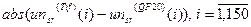 (б); гистограмма значений
(б); гистограмма значений 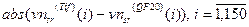 (в)
(в)
В таблице 8.4 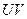 ,
, 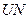 ,
, 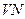 – это средние значения по всем тестируемым изображениям глобальных максимумов гистограмм значений углов между СНВ
– это средние значения по всем тестируемым изображениям глобальных максимумов гистограмм значений углов между СНВ  и
и  ,
,  и n-оптимальным,
и n-оптимальным,  и n-оптимальным соответственно, выраженные в градусах;
и n-оптимальным соответственно, выраженные в градусах; 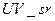 ,
, 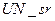 ,
, 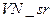 — средние значения по всем тестируемым ЦИ
— средние значения по всем тестируемым ЦИ 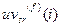 ,
, 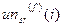 ,
, 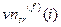 ,
, 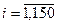 , соответственно, выраженные в градусах.
, соответственно, выраженные в градусах.
Таблица 8.4 –
Характеристики взаимного расположения сингулярных векторов  ,
,  и n-оптимального вектора
и n-оптимального вектора
| Формат ЦИ | 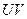
| 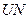
| 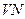
| 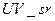
| 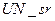
| 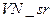
| |
| TIF | 0,88 | 0,77 | 0,66 | 5,84 | 4,29 | 3,76 | |
| JPEG | 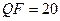
| 0,61 | 0,48 | 0,31 | 5,89 | 4,31 | 3,74 |
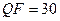
| 0,65 | 0,55 | 0,39 | 5,91 | 4,33 | 3,76 | |
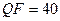
| 0,78 | 0,58 | 0,39 | 5,95 | 4,36 | 3,80 | |
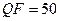
| 0,84 | 0,60 | 0,51 | 5,95 | 4,36 | 3,81 | |
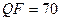
| 0,85 | 0,70 | 0,58 | 5,88 | 4,32 | 3,78 | |
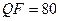
| 0,86 | 0,74 | 0,66 | 5,87 | 4,32 | 3,78 | |
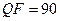
| 0,89 | 0,77 | 0,69 | 5,88 | 4,32 | 3,72 |
Из табл.8.4 видно, что все рассмотренные в ходе эксперимента характеристики ( 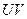 ,
, 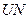 ,
, 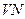 ,
, 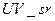 ,
, 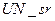 ,
, 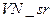 ) взаимного расположения векторов
) взаимного расположения векторов  ,
,  , n-оптимального сравнимы для различных форматов и различного качества сжатия. Дополнительным подтверждением этого являются результаты, представленные в таблице 8.5, полученные в ходе вычислительного эксперимента, в котором тестировалось 300 цифровых изображений в формате без потерь (TIF), 300 изображений в формате JPEG, полученных различными фотокамерами (без привязки к коэффициенту сжатия), 300 изображений в формате JPEG2000, полученных при помощи пересохранения ЦИ из первой группы (TIF).
, n-оптимального сравнимы для различных форматов и различного качества сжатия. Дополнительным подтверждением этого являются результаты, представленные в таблице 8.5, полученные в ходе вычислительного эксперимента, в котором тестировалось 300 цифровых изображений в формате без потерь (TIF), 300 изображений в формате JPEG, полученных различными фотокамерами (без привязки к коэффициенту сжатия), 300 изображений в формате JPEG2000, полученных при помощи пересохранения ЦИ из первой группы (TIF).
Проверим, насколько возмущения СНВ, отвечающих максимальным СНЧ блоков матрицы ЦИ, в пределах окрестности n-оптимального вектора обеспечивают надежность восприятия возмущенного изображения. Для этого в среде MATLAB был проведен вычислительный эксперимент, в котором было задействовано 300 ЦИ (из базы NRCS, которая является традиционной для тестирования стеганоалгоритмов) в разных форматах (с потерями, без потерь). В каждом блоке каждого цифрового изображения сингулярные векторы  или
или (какой именно из них, выбиралось случайным образом) поворачивался до совпадения с n-оптимальным. Полученные в результате ЦИ сохранялись в формате без потерь (BMP). Эти ЦИ сохраняли надежность восприятия, устанавливаемую путем субъективного ранжирования, при этом среднее значение
(какой именно из них, выбиралось случайным образом) поворачивался до совпадения с n-оптимальным. Полученные в результате ЦИ сохранялись в формате без потерь (BMP). Эти ЦИ сохраняли надежность восприятия, устанавливаемую путем субъективного ранжирования, при этом среднее значение 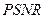 составило по 300 ЦИ34.7 dB. Типичный иллюстративный пример приведен на рис.8.8, где при описаном возмущении ЦИ
составило по 300 ЦИ34.7 dB. Типичный иллюстративный пример приведен на рис.8.8, где при описаном возмущении ЦИ 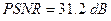 .
.
Таблица 8.5
Характеристики взаимного расположения сингулярных векторов  ,
,  и n-оптимального вектора при различных форматах хранения цифрового изображени
и n-оптимального вектора при различных форматах хранения цифрового изображени
| Формат ЦИ | 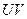
| 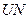
| 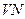
| 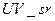
| 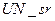
| 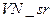
| |
| TIF | 0,90 | 0,76 | 0,64 | 5,89 | 4,41 | 3,87 | |
| JPEG | 0,94 | 0,80 | 0,62 | 5,97 | 4,31 | 3,80 | |
| JPEG2000 | 0,91 | 0,75 | 0,61 | 6,30 | 5,09 | 4,53 |
Таким образом, в результате проведенного качественного и количественного анализа возмущений сингулярных векторов блоков матрицы ЦИ при сжатии доказано следующее утверждение, носящее качественный характер.
Утверждение. Для того, чтобы стеганоалгоритм был устойчивым к возмущающим воздействиям достаточно, чтобы процесс стеганопреобразования был организован таким образом, чтобы формальным представлением его являлась совокупность возмущений левых и/или правых сингулярных векторов блоков матрицы контейнера, отвечающих максимальным сингулярным числам ( 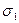 ) блоков, при этом возмущения сингулярных векторов, происходящие в результате погружения ДИ, должны оставлять их в малой окрестности n-оптимального вектора, что обеспечит надежность восприятия сформированного стеганосообщения. Если же при формальном представлении стеганопреобразования в виде совокупности возмущений сингулярных векторов блоков матрицы контейнера эти возмущения будут отвечать сингулярным векторам для которых сингулярные числа имеют малую отделенность, то сформированное стеганосообщение окажется чувствительным, а соответствующий стеганоалгоритм неустойчивым к сжатию.
) блоков, при этом возмущения сингулярных векторов, происходящие в результате погружения ДИ, должны оставлять их в малой окрестности n-оптимального вектора, что обеспечит надежность восприятия сформированного стеганосообщения. Если же при формальном представлении стеганопреобразования в виде совокупности возмущений сингулярных векторов блоков матрицы контейнера эти возмущения будут отвечать сингулярным векторам для которых сингулярные числа имеют малую отделенность, то сформированное стеганосообщение окажется чувствительным, а соответствующий стеганоалгоритм неустойчивым к сжатию.
Замечание. Необходимо заметить, что возмущения сингулярных векторов, отвечающих максимальным сингулярным числам блоков, нельзя рассматривать обособленно от возмущений остальных СНВ блоков, поскольку в силу ортормированности всех СНВ блока возмущение  (
(  ) необходимо приведет к возмущению всех остальных, что увеличит величину возмущения всего блока (и это произойдет безотносительно к процессу стеганопреобразования). Поэтому при организации процесса погружения ДИ необходимо будет для конкретных разрабатываемых стеганоалгоритмов обеспечить процесс приведения всех сингулярных векторов к ортонормированному виду так, чтобы за счет этого приведения величина
) необходимо приведет к возмущению всех остальных, что увеличит величину возмущения всего блока (и это произойдет безотносительно к процессу стеганопреобразования). Поэтому при организации процесса погружения ДИ необходимо будет для конкретных разрабатываемых стеганоалгоритмов обеспечить процесс приведения всех сингулярных векторов к ортонормированному виду так, чтобы за счет этого приведения величина 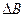 возросла незначительно.
возросла незначительно.

а

б
Рис.8.8. Результат возмущения в каждом блоке цифрового изображения сингулярного вектора, отвечающего максимальному сингулярному числу блока: исходное ЦИ (а); возмущенное ЦИ (б)
Из предыдущих утверждений следует истинность следующего утверждения.
Утвержение. Для того, чтобы стеганоалгоритм был устойчивый к возмущающим воздействиям, достаточно, чтобы процесс стеганопреобразования проводился таким образом, чтобы при формальном представлении его результата в виде совокупности возмущений сингулярных чисел и/или сингулярных векторов блоков, эти совокупности содержали возмущения максимальных СНЧ блоков и/или СНВ, отвечающих максимальным СНЧ блоков.
Замечание. Истинность полученных утверждений не зависят от того, в какой области контейнера (пространственной, частотной) происходило стеганопреобразование. Это вытекает из возможности формального представления произвольного СП в виде 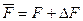 , где
, где  — матрица контейнера,
— матрица контейнера, 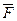 — матрица стеганосообщения.
— матрица стеганосообщения.
Замечание. Полученные теоретические заключения могут быть использованы для организации анализа любого из существующих стеганоалгоритмов с точки зрения его устойчивости к возмущающим воздействиям. Для этого необходимо результат стеганопреобразования представить в виде совокупности возмущений СНЧ и/или СНВ блоков матрицы контейнера и воспользоваться предыдущими утверждениями.
Вопросы
1. Свойства сингулярных чисел матрицы цифрового изображения.
2. Как чаще всего моделируется возмущающее воздействие на цифровое изображение?
3. Как может вычисляься энергия цифрового изображения?
4. Какая зона сингулярного спектра называется мертвой зоной?
5. Всегда ли на практике будут сингулярные числа, для которых возмущение будет в точности равно нулю после возмущающего воздействия?
6. Основные свойства сингулярных векторов матрицы цифрового изображения.
7. Что такое достаточная (недостаточная) отделенность сингулярного числа 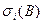 блока
блока  по отношению к возмущению
по отношению к возмущению 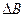 ?
?
8. Чем определяется характер поведения сингулярного вектора блока матрицы цифрового изображения, соответствующего максимальному сингулярному числу?
9. Как связаны собственные значения матриц 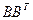 и
и 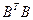 с сингулярными числами матрицы
с сингулярными числами матрицы  ?
?
10. Какой вектор называемый n-оптимальным вектором? Его свойства.
11. Достаточное условие устойчивости стеганоалгоритма к возмущающим воздействиям. Обосновать.
Литература
3. Кобозєва А.А. Аналіз захищеності інформаційних систем / Кобозєва А.А., Хорошко В.А., Мачалін І.О. – К.: Вид.ДУІКТ, 2010. – 316 с.
4. Кобозева А.А. Анализ информационной безопасности / А.А.Кобозева, В.А.Хорошко. – К.: Изд. ГУИКТ, 2009. – 251 с.
5. Гонсалес Р. Цифровая обработка изображений / Р.Гонсалес, Р.Вудс; пер. с англ. под ред. П.А.Чочиа. — М.: Техносфера, 2005. — 1072 с.
6. Каханер Д. Численные методы и программное обеспечение / Д.Каханер, К.Моулер, С.Нэш; пер. с англ. Х.Д.Икрамова. — М.: Мир, 2001. — 575 с.
7. Гантмахер Ф.Р. Теория матриц / Ф.Р.Гантмахер. — М.: Наука, 1988. — 552 с.
8. Грибунин В.Г. Цифровая стеганография / В.Г.Грибунин, И.Н.Оков, И.В.Туринцев. — М.: Солон-Пресс, 2002. — 272с.
9. Стеганография, цифровые водяные знаки и стеганоанализ : [монография] / А.В. Аграновский, А.В. Балакин, В.Г. Грибунин, С.А. Сапожников. — М.: Вузовская книга, 2009. — 220 с.
10. Кобозева А.А. Применение сингулярного и спектрального разложения матриц в стеганографических алгоритмах / А.А.Кобозева // Вісник Східноукр-го нац-го ун-ту ім. В.Даля. — 2006. — №9(103), ч.1. — С.74—82.
11. Кобозева А.А. Учет свойств нормального спектрального разложения матрицы контейнера при обеспечении надежности восприятия стегосообщения / А.А.Кобозева, Е.А.Трифонова // Вестник НТУ «ХПИ». — 2007. — №18. — С.81—93.
12. Кобозева А.А. Оценка чувствительности стегосообщения к возмущающим воздействиям / А.А.Кобозева, Е.В.Нариманова // Системні дослідження та інформаційні технології. – 2008. - №3. – С. 52-65.
13. Miller, A. Least Significant Bit Embeddings: Implementation and Detection [Электронный ресурс]: Computer Science Honors Thesis. – 2012. – Режим доступа: http://aaronmiller.in/thesis.
14. Кобозева, А.А. Общий подход к анализу состояния информационных объектов, основанный на теории возмущений / А.А. Кобозева // Вісник Східноукраїнського національного університету ім. В. Даля. — 2008. — №8(126), Ч.1. — С. 72–81.
Лекция 9. ОБЕСПЕЧЕНИЕ НЕЧУВСТВИТЕЛЬНОСТИ СТЕГАНОСООБЩЕНИЯ К ВОЗМУЩАЮЩИМ ВОЗДЕЙСТВИЯМ
(продолжение)
План
1. Использование особенностей возмущений сингулярных чисел матрицы цифрового изображения при организации стеганографического канала связи.
2. Стеганолгоритмы, устойчивые к сжатию.
- Использование особенностей возмущений сингулярных чисел матрицы цифрового изображения при организации стеганографического канала связи
Учитывая, что, как уже отмечалось раньше, подходящей моделью для ошибок квантования, возмущающих воздействий при пересылке в канале связи и (или) атак на СС является аддитивный гауссовский шум, при котором наличие МЗСНЧ является практически обязательным, становится очевидным еще одно достаточное условие для обеспечения нечувствительности стеганосообщения к возмущающим воздействиям:
Утверждение. Для того, чтобы используемый при организации стеганографического канала связи стеганометод был устойчивым к возмущающим воздействиям, т.е. генерируемое им СС было нечувствительным, достаточно, чтобы погружение секретной информации можно было формально представить в виде возмущений СНЧ матрицы контейнера, принадлежащих МЗСНЧ.
Таким образом, в качестве области для погружения секретной информации достаточно использовать часть полного набора параметров, определяющих контейнер (некоторые подобласти контейнера), степень нечувствительности которых к возмущающим воздействиям максимальна – СНЧ матрицы контейнера, принадлежащие МЗСНЧ.
Основные шаги метода погружения секретной информации в контейнер выглядят следующим образом:
Шаг 1. Матрица контейнера разбивается на подобласти, количество которых выбирается с учетом длины погружаемого секретного сообщения, при этом количество и непосредственный способ разбиения может использоваться в качестве секретного ключа. Для каждой подобласти вычисляются СНЧ.
Шаг 2. На матрицу контейнера накладывается шум (аддитивный гауссовский шум).
Шаг 3. Возмущенная наложенным шумом матрица разбивается аналогичным шагу 1 образом на подобласти. Для каждой подобласти вычисляются СНЧ.
Шаг 4 (локализация области контейнера для погружения секретной информации). Для каждой из подобластей контейнера определяются СНЧ, входящие в МЗСНЧ этой подобласти (это можно сделать, либо определяя окрестность точки персечения интерполяционных сплайнов сингулярных спектров исходной и возмущенной подобласти, либо определяя область нулевых (сравнимых с нулем) возмущений СНЧ после наложения шума).
Шаг 5 (погружение секретной информации). Погружение секретной информации производится таким образом, чтобы при стеганопреобразовании возмущению подверглись только СНЧ выделенных подобластей контейнера, входящие в МЗСНЧ, а остальные элементы полных наборов параметров, определяющих подобласти, остались без изменения.
Для извлечения секретной информации шаги 1-4 предпринимаются для матрицы стеганосообщения, результатом чего на шаге 4 будет локализация области стеганосообщения, которая была использована для погружения. На шаге 5 извлечение информации происходит из СНЧ, находящихся в определенной на предыдущих шагах МЗСНЧ с учетом алгоритма, использованного для погружения.
Для аппробации одной из конкретных реализаций предложенного метода в среде Matlab был проведен очередной этап вычислительного эксперимента, где использовались в качестве контейнеров 200 изображений. Секретное сообщение генерировалось случайным образом в виде бинарной последовательности. Погружение на шаге 5 осуществлялось аддитивно непосредственно в СНЧ из МЗСНЧ. С учетом того, что МЗСНЧ локализуется в верхней части сингулярного спектра, бинарное секретное сообщение кодировалось в алфавите 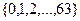 , что уменьшило количество погружаемых элементов сообщения в 6 раз.
, что уменьшило количество погружаемых элементов сообщения в 6 раз.
Эффективность декодирования, определяемая как
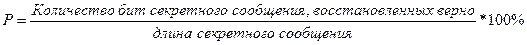
для различных изображений составила от 80% до 98%, а в среднем – 94.7%.
Проведенный в работе анализ характера возмущений СНЧ матриц, отвечающих изображениям, при различных возмущающих воздействиях дал возможность для получения достаточного условия обеспечения нечувствительности стеганосообщения и может использоваться как теоретический базис для созданий устойчивых стеганографических алгоритмов, что подтверждается приведенными результатами вычислительного эксперимента.
- Стеганолгоритмы, устойчивые к сжатию
Стеганографический метод, использующий формализацию стеганопреобразования в виде совокупности возмущений сингулярных чисел.На основе полученных теоретических выводов предлагается следующий стеганографический метод. В качестве ДИ рассматривается последовательность 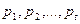 , где
, где 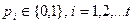 . Декодированную ДИ будем обозначать:
. Декодированную ДИ будем обозначать: 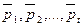 , где
, где 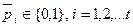 .
.
Погружение ДИ.
Шаг 1. Матрица  контейнера разбивается стандартным образом на блоки
контейнера разбивается стандартным образом на блоки  размером
размером 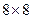 . Такое разбиение выбрано в силу того, что оно является стандартным при организации сжатия. Каждый блок контейнера используется для погружения
. Такое разбиение выбрано в силу того, что оно является стандартным при организации сжатия. Каждый блок контейнера используется для погружения 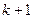 (
( 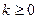 ) бит ДИ.
) бит ДИ.
Шаг 2. (Погружение ДИ в очередной блок контейнера). Пусть  — очередной блок, используемый для стеганопреобразования, а
— очередной блок, используемый для стеганопреобразования, а 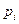 ,...,
,..., 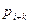 — очередные биты ДИ.
— очередные биты ДИ.
2.1. Каким-либо алгоритмом определяются СНЧ 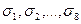 блока
блока  ,
, 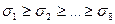 ;
;
2.2. В зависимости от следующих условий
― требуемого значения скрытой пропускной способности организуемого канала связи,
― соотношения между значениями 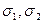 для конкретного блока
для конкретного блока  ,
,
― значений 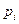 ,...,
,..., 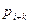 – погружаемых в
– погружаемых в  бит ДИ
бит ДИ
погружение дополнительной информации производится за счет взаимной корректировки значений 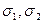 . Количество различных вариантов корректировки определяется количеством различных вариантов упорядоченных бинарных последовательностей
. Количество различных вариантов корректировки определяется количеством различных вариантов упорядоченных бинарных последовательностей 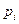 ,...,
,..., 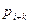 :
: 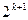 ;
; 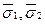 - возмущенные после СП значения
- возмущенные после СП значения 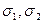 соответственно.
соответственно.
Шаг 3. (Формирование блока 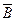 СС с матрицей
СС с матрицей 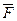 ). Соответствующий
). Соответствующий  блок СС
блок СС 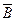 формируется с учетом возмущенных СНЧ
формируется с учетом возмущенных СНЧ 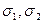 : сингулярные числа
: сингулярные числа 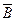 — это
— это 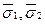 ,
, 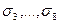 .
.
Декодирование ДИ.
Шаг 1. Матрица 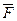 стеганосообщения разбивается стандартным образом на блоки
стеганосообщения разбивается стандартным образом на блоки 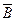 размером
размером 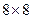 . Каждый блок используется для декодирования
. Каждый блок используется для декодирования 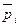 ,...,
,..., 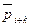 — значений бит ДИ.
— значений бит ДИ.
Шаг 2. (Декодирование ДИ из очередного блока СС). Пусть 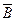 — очередной блок, из которого извлекаются биты
— очередной блок, из которого извлекаются биты 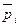 ,...,
,..., 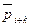 ДИ.
ДИ.
2.1. Определяются СНЧ 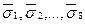 блока
блока 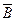 .
.
2.2. Определяется связь между значениями 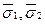 , в соответствии с которой целиком декодируется бинарная последовательность
, в соответствии с которой целиком декодируется бинарная последовательность 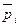 ,...,
,..., 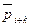
Конкретный способ реализации шагов 2 при погружении и декодировании ДИ будет определять конкретный стеганоалгоритм, один из вариантов которого предлагается в следующем подразделе.
Стеганоалгоритм, основанный на возмущении максимальных сингулярных чисел блоков контейнера.Рассмотрим конкретную реализацию предложенного выше стеганометода в виде стеганоалгоритма.
В качестве ОС может выступать как цветное ЦИ, так и изображение в градациях серого. Для цветного ЦИ погружение ДИ будет производиться в матрицы 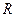 ,
, 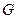 ,
,  .
.
Обозначим через 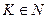 , где
, где 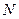 - множество натуральных чисел, пороговое значение вариации возмущений максимальных СНЧ, смысл которого будет объяснен ниже. Основные шаги предлагаемого стеганоалгоритма, обозначаемого далее
- множество натуральных чисел, пороговое значение вариации возмущений максимальных СНЧ, смысл которого будет объяснен ниже. Основные шаги предлагаемого стеганоалгоритма, обозначаемого далее 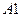 , выглядят следующим образом.
, выглядят следующим образом.
Погружение ДИ.
Шаг 1. Матрица  контейнера разбивается стандартным образом на блоки
контейнера разбивается стандартным образом на блоки  размером
размером 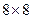 . Каждый блок используется для погружения 1 бита
. Каждый блок используется для погружения 1 бита 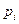 ДИ (
ДИ ( 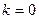 ).
).
Шаг 2. (Погружение бита ДИ). Пусть  — очередной блок, используемый для СП, а
— очередной блок, используемый для СП, а 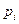 — очередной бит ДИ.
— очередной бит ДИ.
2.2. Строится сингулярное разложение 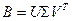 , где
, где 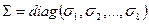 ;
;
2.3. Если
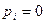
то
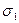 корректируется так, чтобы целая часть разности между
корректируется так, чтобы целая часть разности между 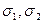 при делении на
при делении на 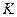 давала остаток
давала остаток 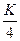 . Результат корректировки – возмущенное максимальное СНЧ
. Результат корректировки – возмущенное максимальное СНЧ 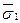 ;
;
Иначе
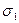 корректируется так, чтобы целая часть разности между
корректируется так, чтобы целая часть разности между 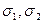 при делении на
при делении на 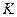 давала остаток
давала остаток 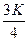 . Результат —
. Результат — 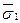 .
.
Шаг 3. (Формирование блока СС 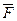 ). Соответствующий
). Соответствующий  блок СС
блок СС 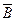 вычисляется как:
вычисляется как:
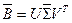 ,
,
где 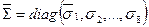 .
.
Декодирование ДИ.
Шаг 1. Матрица 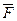 стеганосообщения разбивается стандартным образом на блоки
стеганосообщения разбивается стандартным образом на блоки 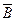 размером
размером 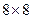 . Каждый блок используется для декодирования 1 бита ДИ.
. Каждый блок используется для декодирования 1 бита ДИ.
Шаг 2. (Декодирование бита ДИ). Пусть 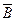 — очередной блок, из которого извлекается бит
— очередной блок, из которого извлекается бит 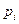 ДИ.
ДИ.
2.2. Строится сингулярное разложение 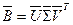 , где
, где 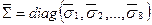 ;
;
2.3. Если
целая часть разности между 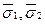 при делении на
при делении на 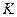 дает остаток меньше
дает остаток меньше 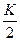
то
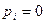 ;
;
Иначе
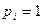 .
.
Замечание. Необходимо отметить, что сингулярное разложение на шагах 2.2 погружения и декодирования ДИ не обязано быть нормальным. Нормальность сингулярного разложения обеспечивает его единственность, в то время, как обычное сингулярное разложение определяется неединственным образом за счет неединственности сингулярных векторов. Однако сингулярные числа для  и
и 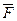 , которые и используются в алгоритме
, которые и используются в алгоритме 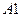 , определяются однозначно в каждом из упомянутых сингулярных разложений.
, определяются однозначно в каждом из упомянутых сингулярных разложений.
Рассмотрим подробно пороговое значение вариации возмущений максимальных СНЧ 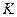 . Исходя из приведенных выше результатов, значительную устойчивость предложенного алгоритма можно было бы ожидать в случае
. Исходя из приведенных выше результатов, значительную устойчивость предложенного алгоритма можно было бы ожидать в случае 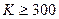 . Тогда остатки от деления
. Тогда остатки от деления 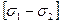 , например, для
, например, для 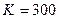 , могут принимать значения из множества
, могут принимать значения из множества 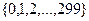 . При погружении
. При погружении 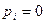 СНЧ
СНЧ 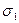 очередного блока становится таким, что остаток от деления
очередного блока становится таким, что остаток от деления 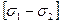 на
на 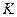 равен 75, для
равен 75, для 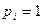 упомянутый остаток будет равен 225 (рис.9.1). Исходя из возможного максимального возмущения
упомянутый остаток будет равен 225 (рис.9.1). Исходя из возможного максимального возмущения 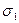 при сжатии с
при сжатии с 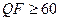 (
( 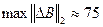 ) и конкретики алгоритма декодирования ДИ, сжатие с
) и конкретики алгоритма декодирования ДИ, сжатие с 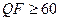 с большой вероятностью не сможет вывести значение СНЧ
с большой вероятностью не сможет вывести значение СНЧ 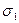 за пределы «зоны», отвечающей погруженному биту дополнительной информации (рис.9.1).
за пределы «зоны», отвечающей погруженному биту дополнительной информации (рис.9.1).
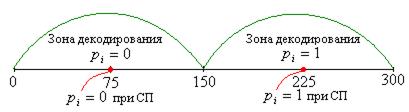
Рис.9.1. Иллюстрация процессов погружения и декодирования дополнительной информации при 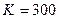
Однако, как показал вычислительный эксперимент, значение 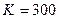 , используемое в процессе стеганопреобразования, не всегда обеспечивало надежность восприятия стеганосообщения, которая устанавливалась путем субъективного ранжирования. Заметим, что хотя максимальное значение возмущения блока рассматривалось как
, используемое в процессе стеганопреобразования, не всегда обеспечивало надежность восприятия стеганосообщения, которая устанавливалась путем субъективного ранжирования. Заметим, что хотя максимальное значение возмущения блока рассматривалось как 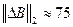 , полученное для
, полученное для 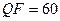 , не имеет смысла выяснять максимальное значение
, не имеет смысла выяснять максимальное значение 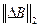 для
для 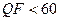 : очевидно, что в этих случаях
: очевидно, что в этих случаях 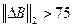 , однако увеличение значения
, однако увеличение значения 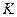 в силу вышесказанного не представляется возможным.
в силу вышесказанного не представляется возможным.
Уменьшение 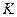 до 250 не обеспечило надежность восприятия стеганосообщения. В вычислительном эксперименте, проводимом в среде MATLAB для более, чем 400 ЦИ-контейнеров, хр
до 250 не обеспечило надежность восприятия стеганосообщения. В вычислительном эксперименте, проводимом в среде MATLAB для более, чем 400 ЦИ-контейнеров, хр
Дата добавления: 2016-07-22; просмотров: 2099;











