Відображення інформації у цифровій техніці
МАТЕМАТИЧНІ ОСНОВИ ЦИФРОВОЇ ТЕХНІКИ
Інформація (від лат informatio – роз’яснення, виклад, обізнаність) як об’єкт передання, поширення, перетворення, зберігання чи безпосереднього виконання потребує матеріального носія. Таким носієм інформації у радіоелектроніці е електричний сигнал - напруга або струм. Як функція часу електричний сигнал може бути неперервним або дискретним. Неперервний (або аналоговий) сигнал у заданому діапазоні зміни аргументу t набуває довільної множини значень, дискретний сигнал - лише при певних значеннях аргументу nt (де t - інтервал дискретності, n = 0,1,2,...). Тому дискретний сигнал може мати тільки обмежене (скінченне) число рівнів напруги або струму. Ці рівні зафіксовані на однакових інтервалах часу nt , що називаються тактами (в музиці, до речі, тактами також називають інтервали часу, хоча там вони можуть бути не обов’язково однакової розмірності).У ЦТ основним носієм інформації є дискретний сигнал. Щоб він адекватно відображав інформацію, яка може бути подана у найрізноманітніших формах (числами, буквами, сигналами різної природи чи якимись символами), число рівнів і значення їх величин мають підпорядковуватися певній системі відліку, тобто системі числення, що характеризується певною сукупністю символів (алфавітом) і правил. Людина у повсякденному житті користується десятковою (арабською) системою числення, що складається з 10 цифр (0...9). Здавалося б, що й для відображення інформації з допомогою дискретного сигналу найкраще підходить десяткова система числення - досить лише мати шкалу з десяти однакових за величиною рівнів (квантів) напруг. Проте вона не стала основною в ЦТ з багатьох причин. Цифрові сигнали, створені на основі десяткової системи числення, технічно реалізувати досить важко і тому економічно невигідно, бо такого типу цифрові пристрої повинні мати десять рівнів напруги.
Найпростішою з усіх позиційних систем числення є двійкова , або бінарна система, що складається з двох цифр: 0 і 1. Звідси й походження слова-терміна "біт" , що означає "двійкова цифра” тобто 0 або 1. Двійкова система дозволяє найефективніше відобразити інформацію з допомогою електричних цифрових сигналів, якщо, наприклад, низький рівень напруги або відсутність імпульсу позначити як логічний нуль (лог. 0), а високий рівень напруги або наявність імпульсу - як логічну одиницю (лог.1).
Всю інформацію, таким чином, можна зобразити у вигляді ланцюжка 0 і 1, тобто набору чи комбінації бітів, що називають словом. Отже, послідовність 0 і 1 певної довжини (слово) може зображати будь-яке число, кожний розряд (біт) якого з одиницею інформації.
Задана кількість двійкових розрядів - бітів може не відповідати обсягу інформації, яка також вимірюється у бітах. Це дуже часто є причиною непорозумінь (через плутання цих двох різних понять). У цифровій та обчислювальній техніці 1 біт означає один двійковий розряд - символ, що може набувати лише ціле число, тобто двійкове n - розрядне число, що дорівнює n біт. Але щодо обсягу інформації n-бітне число не обов’язково може мати n біт інформації, воно цілком може дорівнювати, наприклад, 0.76 біт або 0.1 біт. Як правило, чим менше число бітів (як двійкових розрядів) використовується для відображення певної інформації, тим більша густина інформації. Наприклад (див.таб.1.1):
Таблиця 1.1 Однакова кількість інформації в різнопозиційних числах
| число з 4 позиціями | число з 1 позицією | число з 2 позиціями |
З допомогою двійкових чисел у цифровій та мікропроцесорній техніці зображаються дані - відомості, факти тощо, все те, що необхідно для виконання певної дії.
Таблиця 1.2 Кодування в поширених системах числення
| “2” | “8” | “10” | “16” |
| ….. | …. | ….. | А B C D E F ….. 1А 1В |
Дані подаються у такому (формалізованому) вигляді, що після перетворення у фізичний носій інформації вже у вигляді цифрового сигналу їх можна передавати, обробляти і зберігати за допомогою технічних носіїв чи засобів. Тому дуже часто замість слова "дані" вживається слово "інформація". Набір правил, що розкриває спосіб зображення даних з допомогою умовних знаків чи символів, називається кодом . Носіями інформації в електронних обчислювальних пристроях (ЕОП) є електричні сигнали, найчастіше — напруги. Інформація обробляється в цифровій формі. Кожній цифрі ставиться у відповідність визначений рівень сигналу.
Одиницею зображення даних, а також обміну даними, якою як єдиним цілим оперують між собою окремі цифрові пристрої чи вузли, є восьмирозрядне (восьмибітне) двійкове число - байт. Отже, 1 байт = 8 біт, і, очевидно, що з допомогою такого слова можна передати одне з 28 = 256 різних повідомлень, тобто можна, наприклад, закодувати текст якоюсь мовою, де кожному символу (букві, розділовому знаку, цифрі тощо) має відповідати одна кодова комбінація з 8 біт, або 1 байт. На практиці доцільно знати і вміти користуватися (наприклад, для визначення обсягу пам’яті ЕОМ) такими одиницями інформації.
Систем числення може бути безліч. (Поряд із згаданими системами у пристроях ЦТ можна зустріти й такі, як, наприклад, трійкова (Р=З). Очевидно, що вибір тої чи іншої системи числення залежить від певних критеріїв, які мають виконуватись для забезпечення оптимального результату. В загальному довільне число А у позиційній системі числення з постійною основою Р може бути виражене числовим рядом:
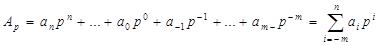 ( 1.0)
( 1.0)
де 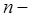 число знаків до коми;
число знаків до коми; 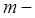 число знаків після коми;
число знаків після коми; 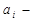 число в і-му розряді;
число в і-му розряді; 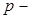 вага і-го розряду;
вага і-го розряду;
Двійкова система має набір цифр {0,1}, тому 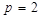 . Довільне число в А2 у двійковій системі можна зобразити виразом (1.1), результат обчислення якого – представлення цього числа в десятковій системі числення. Наприклад:
. Довільне число в А2 у двійковій системі можна зобразити виразом (1.1), результат обчислення якого – представлення цього числа в десятковій системі числення. Наприклад:
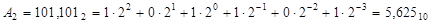
Для практичних розрахунків слід запам’ятати значення перших 13-ти розрядів цифр двійкової системи числення:
20=1, 21=2, 22=4, 23=8, 24=16, 25=32, 26=64, 27=128,
28=256, 29=512, 210=1024, 211=2048, 212=4096;
Шістнадцяткова система має набір цифр {0,1,2,3,4,5,6,7,8,9,А,B,C,D,E,F}, тому 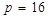 .При цьому великими буквами латинського алфавіту зображені цифри 10,11,12,13,14,15 (10). Наприклад:
.При цьому великими буквами латинського алфавіту зображені цифри 10,11,12,13,14,15 (10). Наприклад:
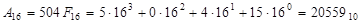
Для практичних розрахунків слід запам’ятати значення перших 6-ти розрядів цифр шістнадцяткової системи числення:
160=1, 161=16, 162=256, 163=4096, 164=65535, 165=1048576
Десяткова система числення, якою користуємось у повсякденному житті, не є найкращою з точки зору її технічної реалізації у цифрових пристроях. Відомі на сьогодні елементи, що мають десять стійких станів, щоб розрізнити всі десять символів (рівнів), наприклад, декатрони, мають невисоку швидкодію та складні для виготовлення. Отже, виникає закономірне питання: яка система числення найкраща? Вчені довели, що раціональною з точки зору мінімальних витрат умовного обладнання є система числення з основою Р»2.72»3. Отже, трійкова система краща за двійкову. Однак з’ясувалося, що за такими характеристиками цифрових пристроїв, як швидкодія, об’єм пам’яті, техніка виконання арифметичних та логічних операцій, найкращою е двійкова система числення.
Розглянемо, чому крім десяткової та двійкової систем числення в цифровій схемотехніці використовуються ще й такі системи числення, як вісімкова, шістнадцяткова і т. ін. Справа в тому, що якщо нас цілком влаштовує десяткова система, а для цифрового пристрою (мікропроцесорів, ЕОМ тощо) - виключно двійкова, бо там інформація обробляється тільки за допомогою нулів і одиниць, то проміжною, сполучною ланкою між нами і цифровим пристроєм має бути така система числення, яка була б найзручнішою як для взаємного переводу обох систем, так і для забезпечення простої технічної реалізації процедури. Для цього власне використовують проміжні системи числення - коди, за допомогою яких можна уникнути довгих ланцюжків з нулів та одиниць, які властиві двійковій системі. До таких систем кодування належить двійково-десятковий код (ДЦК).
Особливість ДДК полягає в тому, що кожній десятковій цифрі даного розряду відповідав чотирибітове (група з чотирьох бітів) двійкове число - тетрада. Наприклад, об’єднання двох тетрад дає можливість зобразити двозначне десяткове число, а з точки зору інформативності - реалізувати 16х16 - 256 двійкових комбінацій. При такому числі комбінацій можна закодувати не тільки 80 різних друкованих знаків клавіатури друкарської машинки, але й усі букви латинського алфавіту, розділові знаки, різні символи тощо.
Але при перетворенні десяткових чисел ДДК має надлишковість, бо при групуванні тетрадами шість комбінацій відпадає. Водночас при групуванні тріадами (трьома бітами), навпаки, інформативність падає. Цей факт і пояснює зручність шістнадцяткової системи числення, бо для ДЦК як разі потрібно 16 бітових комбінацій, які повністю забезпечує одна тетрада (11112=152). Зрозуміло, що при групуванні тріадами найзручнішою буде вісімкова система числення - там як раз вистачає 8 бітових комбінацій (1112=710)
Треба мати на увазі, що обидва коди - "16" і "8" - це тільки спосіб зображення двійкових чисел, якими оперують цифрові пристрої та мікропроцесори. Однак з точки зору інформатики код "16" має більші можливості, ніж код "8". Перевага коду "16" над кодом "8" ще в тому, що мікропроцесори маніпулюють словами, які залежно від функціональних можливостей можуть мати набори з 4, 8, 16 або 32 біт.
ДДК називають ще кодом 8-4-2-1, бо ці цифри відповідають вагам розрядів однієї тетради відповідно 23 (старшого розряду), 22, 21 і 20 (молодшого розряду). До двійково-кодованої десяткової системи числення належать й інші системи кодування.
При синтезі таких комбінаційних цифрових пристроїв, як перетворювачі кодів, що призначені для перетворення одного коду в інший, необхідно мати дані про різновиди цих систем кодування.
У табл. 1.3 зведені найбільш поширені в ЦТ різновиди позиційних кодів. До них належать ДДК 8-4-2-1, код 2-4-2-1 (або код Айкена), код з лишком 3 (або код [8-4-2-1]+З), код Грея та циклічний код Джонсона.
ДДК 8-4-2-1, який утворений зображеннями кожної десяткової цифри вагами 23-22-21-20, в найбільш поширеним, тому його найчастіше застосовують для переводу в інший код.
ДДК з лишком 3([8-4-2-1]+З) застосовують для кодування декад при двійково-десятковому зображенні чисел. Особливістю цього коду є те, що всі тетради мають значення на три одиниці більше від тетради коду 8-4-2-1.
Таку властивість самодоповнення має код Айкена (2-4-2-І). Для цього коду ваги розрядів тетради відповідно дорівнюють 21-22-21-20. Таблиця кодування, як видно з табл. 2.2, поділяється на дві частини: 0-4 -_це тетради, що повторюють еквіваленти; 5-9 – кожна тетрада у ДДК має лишок +0110. Така властивість коду Айкена дозволяє довільну цифру одної частини таблиці перетворити на її доповнення до 9 простим інвертуванням.
Особливе місце серед позиційних систем кодування посідають код Грея і циклічний код Джонсона. Це спеціальні коди, які мають непостійні ваги розрядів. Якщо у двійковому коді при переході від зображення одного числа до зображення наступного може відбуватись одночасна зміна цифр у кількох його розрядах, то в кодах Грея і Джонсона сусідні числа відрізняоться цифрою (1 або 0) тільки в одному розряді. Така особливість цих кодів запобігає появі джерела помилки у роботі апаратури у тих випадках, коли здійснюється послідовний перехід (зміна) числа з одного такту в наступний (наприклад, від 6 до 5),
У циклічному коді Джонсона перехід до наступного числа здійснюється шляхом послідовної заміни 0 на 1 до заповнення всіх розрядів одиницями, а потім заміною 1 на 0 до заповнення нулями. Помилки за допомогою кода Джонсона виявляються тоді, коли у "хвилі нулів" цього коду з’являється одна або кілька одиниць, а в "хвилі одиниць" - відповідно один або кілька нулів.
Окреме місце у ЦТ займає кодування алфавітно-цифрової інформації. Сюди належить текстова інформація, що являє собою послідовність алфавітно-цифрових символів, кожний з яких підлягає кодуванню. Щоб не було подвійного тлумачення, тобто щоб кожному символу відповідав тільки один код, застосовують спеціально призначені для цього стандартні коди. Зокрема, найчастіше в ЕОМ типу ІВМ застосовують код ASCII (American Standard Code of Information Interchange-американський стандартний код обміну інформацією), де, наприклад, десятковому числу 1 відповідає код 00010000(25) числу 2 - код 00010001, числу З - код 00010010 тощо, а букві А - код 00011000, букві В код 00011001, букві С - код 00011010 і т. ін.
Таблиця 1.3 Приклади двійкових кодів
| Дес. цифра | ДДК 8-4-2-1 | ДДК 2-4-2-1 | ДДК /8-4-2-1/+3 | Код Грея | Код Джонсона | Обчисл. код двійков. числа | Доповняльний код двійкового числа |
| ….. | 0001 0000 0001 0001 0001 0010 0001 0011 0001 0100 0001 0101 0001 0110 0001 0111 …... …… | 0001 0000 0001 0001 0001 0010 0001 0011 0001 0100 0001 1011 0001 1100 0001 1101 …… …... | 0001 0011 0001 0100 0001 0101 0001 0110 0001 0111 0001 1000 0001 1001 0001 1010 …… …... | ……. | ……. | ….11111 …… | ….00000 …… |
Дата добавления: 2016-07-22; просмотров: 3205;











