При полном переборе в ширину гарантированно нахо-дится целевая вершина, т.к. перебор полный.

Путей достижения цели (целевой вершины) в общем случае очень много. При этом есть возможность выбрать наикрат-чайший путь или самый дешёвый, самый быстрый, самый лёгкий и т.п. путь.Т.е. провести оптимизацию нашей матмо-дели, например, при проектировании информационной систе-мы. Но возможен вариант, когда путь в графе поиска решения окажется бесконечным. Тогда алгоритм никогда не завершится.

Это значит, что можно говорить об областях применения алгоритма. Есть класс задач, для которых метод эффективен. Классикой является задача «лабиринтного поиска» или задача «про обезьяну и банан» или «мышь в лабиринте», впервые решённая Клодом Шенноном. В этой задаче пространство ва-риантов различных действий невелико: «повернуть направо», «повернуть налево», «пройти вперёд» и решение лежит на не-которой заданной, как правило, небольшой глубине.

При переборе в глубину прежде всего следует раскры-вать вершины, построенные последними. Процесс всегда будет идти по самой левой ветке вершин. Для ограниче-ния перебора вводится поня-тие глубины вершины в дере-ве перебора. Глубина корня дерева равна 0, а глубина лю-бой последующей вершины равна 1 плюс глубина верши-ны, непосредственно ей пред-

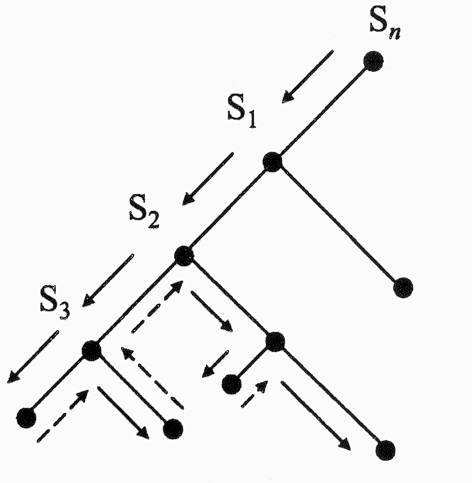
шествующей. Наибольшую глубину всегда будет иметь вер-шина, которая должна быть раскрыта в этот момент време-ни.

Если образующийся путь бесполезен, это значит нераскры-тие целевой вершины при заданной глубине. При этом необ-ходимо вернуться в вершину, предшествующую раскрытой, и попробовать ещё применить к ней операцию раскрытия (процесс возврата на несколько шагов назад называют отка-том назад или бэктрекингом). Это продолжают до тех пор, пока не будет получена целевая вершина.

Возврат реализуют с помощью указателей. В момент, когда при порождении вершин достигается заданная граничная глубина, раскрывается вершина наибольшей глубины, не превышающая этой границы.

Алгоритм перебора в глубину состоит в следующем:

1)раскрывается начальная вершина, соответствующая на-чальному состоянию;

2)раскрывается первая вершина, получаемая в результате раскрытия начальной. Ставится указатель;

3)если она раскрывается, то следующей будет раскры-ваться вновь порождённая вершина. Если вершина не рас-крывается, то процесс возвращается в предыдущую вер-шину;

4)при получении целевой вершины процесс раскрытия завершается и по указателям строится путь, ведущий к корню. При этом по дугам соответствующих операторов получают решение задачи;

5)если для заданной глубины раскрытия целевая верши-на не находится, то весь процесс повторяют снова. В ка-честве новой вершины выбирается самая левая из полу-ченных на предыдущем этапе.

ЭВРИСТИЧЕСКИЕ МЕТОДЫ ПОИСКА
В ПРОСТРАНСТВЕ СОСТОЯНИЙ

Методы полного перебора гарантируют решение задачи, если оно существует. А при наличии нескольких решений гарантирует оптимальное. Однако практически эти методы применимы для задач с графом состояний небольшой раз-мерности. Для реальных случаев чаще всего исполь-зуется допинформация, основанная на предыдущем опыте.Это эвристическая информация(говорили на прошлой лекции); если эвристическая информация органи-зована в правила, то это эвристические правила или эврис-тики. Эвристическая информация носит сугубо специаль-ный характер и может быть применима в рамках задач данного класса. Эвристическая информация делает перебор упорядоченным.

Имеют в виду хорошо известные методы: «ветвей и границ», «метод динамического программирования Беллмана», мето-ды на основе принципа максимума Л.С. Понтрягина.

В качестве примера рассмотрим известную задачу о ком-мивояжёре. Суть её в том, что бродячий торговец должен по-бывать в каждом из N городов точно по одному разу и вер-нуться в исходный город. Желательно, чтобы маршрут был минимальным по протяжённости (см. рисунок на след. слай-де). Второй рисунок более подробно представляет простран-ство состояний.

Начинаем перебор в ширину. На первом уровне получаем возможные пути разной длины: 2, 2, 6, 3. Если придержи-ваться эвристики «на каждом шаге выбирать путь минималь-ной длины», следует выполнить шаги S1-S2 и S2-S3, затем S3-S4 или S3-S5, затем S4-S5 и т.д.

Можно убедиться, что путь, най-денный таким образом не всегда будет самым коротким.

Более правильной была бы эв-ристика «выбирать так, чтобы ми-нимальным был суммарный путь» (принцип Беллмана). СЛЕДСЛАЙД

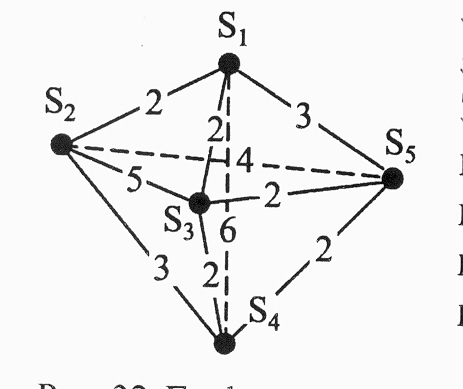
Граф полного перебора, содер-

жащий все возможные пути комми-вояжёра, бу-дет состоять из (N-1)! ва-риантов.

Суть данной проблемы состоит именно в проблеме выбора начальной и последующих вершин при переборе в ширину. Здесь всё сводится к тому, какую вершину на заданном уров-не алгоритм или ЛПР (в частности группа ЛПР) посчитают нужным раскрыть первой, а какие - после. Использование принципа Беллмана (отсылка к ТПР, решение многоступенча-тых задач), поможет найти решение с гораздо меньшими зат-ратами, проходя по графу состояний с конца в начало (к-ц ссылки).

Если же отбросить обратные пути, то получится всего (N-1)!/2. Примеры реальных задач: создание электронных карт размещения передатчиков мобильной связи так, чтобы расстояние до любой точки заданной зоны не превышало Х; разместить банкоматы так, чтобы минимизировать путь инкассатора.

В таких задачах N обычно равняется нескольким десяткам объектам, что для современных компьютеров создаёт серь-ёзную вычислительную проблему.

Эвристические алгоритмы применяют не для поиска единственно правильного или оптимального решения, а для поиска первого решения, удовлетворяющего неко-торому критерию при заданных ограничениях. СЛЕД СЛАЙД

Например, отправляясь в магазин, человек, как правило, не ставит задачу купить самое дешёвое молоко. Он готов купить молоко не ниже заданного качества и не дороже некоторой (нечёткой) оценки и твёрдо не станет тратить на это больше 5 минут (обходить несколько точек).

Не всегда необходимы именно «оптимальные» решения, достаточно найти именно то, которое на данный момент наиболее приемлемо (полностью вписывается в заявлен-ные требования). Если найденное решение хуже, чем рас-считывалось, то ищем дальше, если лучше, значит – заме-чательно, и на этом можно остановиться. Тут необходимо пользоваться правилом – «Лучшее – враг хорошего». Прак-тически все целенаправленные задачи так и решаются. Вспомним пример из военной области с целеустремлён-ностью и целенаправленностью.

В прошлом (1960-1970 годы) разработано много очень полезных эвристик. Причём, что интересно, они не всегда являются очевидными и доказуемыми.

Но при этом позволяют значительно сократить перебор или получить выигрыш в качестве решения. Эти эвристи-ки можно применять не только в продукционной модели. Есть «метод встречной волны» или «двунаправленный перебор от цели к фактам и обратно». Последний метод очень эффективен при анализе противоречивости пост-роенных деревьев.

Графическое представление задач (примеры выше) очень важно для понимания и самой задачи, и метода её решения. Графовое представление отражает взаимосвязи только между объектами предметной области и не отража-ет взаимосвязи между действиями. Или иначе, не заданы отношения между дугами (отношения последовательности и одновременности). Невозможно планирование действий.

ПРЕДСТАВЛЕНИЕ ЗАДАЧИ В ВИДЕ
И-ИЛИ ГРАФА

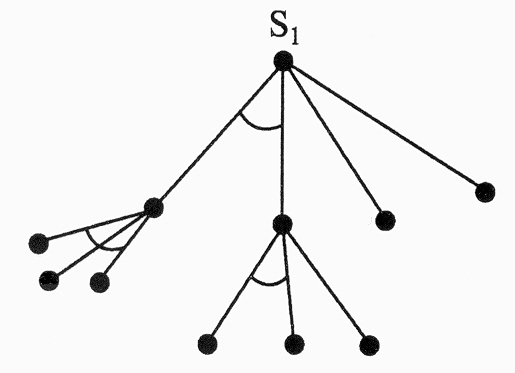
Когда разбивают граф, меж-ду подзадачами могут быть от-ношения согласованности (од-новременности) их решения или отношения И или отноше- ние альтернативности или отношение ИЛИ. На рисунке от-ношение И отмечено дугой, связывающей рёбра графа.

Решения у разных ЛПР практически всегда различны (это связанно с самой природой индивидуального ЛПР), посему у одной и той же задачи может быть множество решений (как рациональных, так и не очень).

В случае с групповым ЛПР, решение всегда сводится к выбору лучшего из предложенных в рамках группы. В большинстве случаев ЛПР руководствуется различного рода эвристиками, что помогает избежать тупиковых вет-вей поиска решений, и/или сокращает время поиска ре-шения.

По данному подходу исходная задача представляется подзадачами, имеющими альтернативный ИЛИ-характер, а сами подзадачи представляются подзадачами с отноше-ниями И. В подобных графах (И-ИЛИ) имеют место от-ношения между подзадачами, которыми являются верши-ны.

Основная цель поиска в И-ИЛИ графе: показать разрешимость вершины S_i.

Вершина является разрешимой, если выполняет-ся одно из следующих условий:

1)вершина S_i является заключительной или терми-нальной;

2)следующие за S_i вершины являются вершинами ИЛИ, и, при этом, хотя бы одна из них разрешима;

3)следующие за S_i вершины являются вершинами И, и, при этом, каждая из них разрешима.

Решающим графом называют подграф, состоящий из разрешимых вершин с корнем в начальной вершине.

Если у вершины И-ИЛИ графа, не являющейся зак-лючительной, нет следующих за ней вершин, то такую вершину называют неразрешимой.

Достоинства и недостатки продукционной модели

Продукционная модель широко применяется в промыш-ленных экспертных системах. Эта модель привлекательна из-за своей наглядности, высокой модульности, лёгкости внесения дополнений и изменений и простоты механизма логического вывода. Продукционные модели очень часто используют из-за наглядности продукций (правил), и прос-тоты понимания логики их функционирования с точки зре-ния пользователя (или проектировщика интел-ных систем).

Продукционные модели могут отображать сценарии (ва-рианты) развития событий в системе.

Простота продукционных моделей и их логики позволя-ют использовать машины вывода, работающие посредством перебора.

Наработан большой арсенал программных средств, реализующих продукционную модель:

1)языки Prolog, Lisp, LOGO, Ops;

2) «оболочки» или «пустые» ЭС – EMYCIN, EXSYS, ESISP, ЭКСПЕРТ;

3)инструментальные системы ПИЭС, СПЭИС и др.

Среди основных достижений советской науки в данной области программа «АЛИЕВ ЛОМИ», которая автомати-чески доказывает теоремы. ЛОМИ означает Ленинград-ское отделение математического института имени В.А. Стеклова.

Есть два основных недостатка продукционной модели.

Первый: при большом числе продукций осложняется проверка непротиворечивости системы продукций. Поэтому, когда добавляются новые продукции, тратится много време-ни на эту проверку.

Второй:продукционному подходу присуща недетерми-нированность или неоднозначность выбора выполняемой продукции из фронта активизируемых продукций. В резуль-тате есть принципиальные трудности при проверке коррект-ности работы системы. Эксперты в области искусственного интеллекта считают, что, если в системе число продукций лежит в диапазоне 1000-1500, то маловероятно, что данная система будет правильно функционировать.

Выбор решения в большинстве случаев становится неоднозначным.

Серьёзные проблемы и более сложные системы не могут быть представлены продукциями, так как данная модель имеет количественное ограничениепо прави-лам представления продукций.

ФРЕЙМЫ ДЛЯ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ

Проблема представления знаний является ключевой проблематикой ИИ. Через представление знаний человек пытается построить модель мира. Но это очень сложная задача по причине многообразия окружающего нас мира. Создать подобную модель практически невозможно, так как нет и не существует достаточного количества знаний о мире.

Одну из наиболее адекватных моделей представления знаний предложил Марвин Мински (профессор компьютер-ных наук в Массачусетском технологическом институте – MIT) в вышедшей в 1974 году книге «Фреймы для пред-ставления знаний». Мышление моделируется на логическом уровне, в отличие от новых систем ИИ (типа нейронных сетей), где моделируется физиологический уровень.

Это делается посредством моделирования связей, а не стереотипов.

Фрейм (по-английски frame) означает рамка, каркас, кадр, скелет. Это структура данныхдля представления стереотипной ситуации. Одна часть показывает, как ис-пользовать данный фрейм, другая – что, скорее всего, произойдёт при его выполнении, третья – что делать, если эти ожидания не реализуются.

На практике областью, где больше всего применяется модель представления знаний, основанная на фреймах, являются объектно-ориентированное программирование и теория объектных БД. Понятие современного объекта языка программирования почти полностью соответствует классическому понятию фрейма.

Главные свойства фреймов, которые используют в языках, это:

инкапсуляция – единство данных и методов в рамках объекта;

наследование – способность объекта пользоваться методами и данными, определёнными в рамках одного из его предков;

полиморфизм – способность объекта в разные момен-ты времени вести себя по-разному (то как объект своего типа, то как объект, аналогичный предкам).

Бывают фреймы-образцы (прототипы, абстрактные кла-ссы), хранящиеся в базе знаний, и фреймы-экземпляры (объекты), которые разрабатывают для отображения ре-альных ситуаций на основе поступающих данных.

Для облегчения поиска фреймов их типизируют или классифицируют. Например, таким образом:

фреймы-структуры – оргструктура предприятия, конструкция дома или технического объекта и т.п.;

фреймы-роли (функциональные обязанности или функции) – директор, инспектор, инженер, усилитель и т.п.;

фреймы-сценарии – бизнес-процесс на предприя-тии, день рождения, проводка какого-то счёта в бухгал-терии, поиск типовой неисправности и т.п.

Записывать фреймы удобно в виде таблиц. Благодаря этому они наилучшим образом подходят для недетерми-нированных процессов, типа баз данных или хранилищ информации.

С теми иди иными издержками фреймовая модель (ФМ) применима для решения любых интеллектуальных задач. Правда тех, решение которых в принципе возможно. Наилучшая область применения ФМ – сложные недетерминированные процессы.

Это такие процессы, исход которых зависит от взаи-модействия большого и очень большого числа различ-ных компонент, объектов и условий. Они же, в свою очередь, могут вести себя по-разному в зависимости от складывающейся ситуации. Моделирование или воспро-изведение таких ситуаций с помощью ФМ отличаетсятем, что процесс развивается в реальном времени в отличие от последовательного развития при продук-ционном подходе.

ФМ имеет ряд весомых преимуществ. Это практи-чески единственная модель, хорошо обоснованная тео-ретически. При практической реализации строится мик-ромир, а исследователь сосредотачивается на свойствах и поведении его участников. Эти участники сами организуют своё взаимодействие на основе правил, при-вычек, сценариев и просто случайностей.

Из-за этого ФМ преодолевает ограничение по раз-мерности, свойственное другим моделям представле-ния знаний, например, продукционной.

В реальном мире постоянно проводится таксоно-мия и сравнения для получения каких-либо выво-дов. Это делается для принятия решений о составлении иерархии или классификации фреймов.

ФМ позволяет хорошо систематизировать иерархию объектов реального мира. Возможно также решение задачи численной таксономии. Численная таксономия — наука о классификации объектов при помощи машинных или математических методов.

Реализуется ФМ на многих языках программирова-ния и на специальном языке FRL (Frame Representation Language), есть примеры успешного применения в ЭС ANALYST, МОДИС.