КІНЦЕВА ШВИДКІСТЬ ЗА МЕТОДАМИ ЛЯЩЕНКА І ФОМЕНКА

П.В. Лященко розробив універсальний метод визначення кінцевої швидкості руху тіл будь-якої крупності, густини і форми в різних режимах. На основі діаграми Релея побудована в логарифмічних координатах діаграма Re²ψ= f(Re) (рис. 2.2).

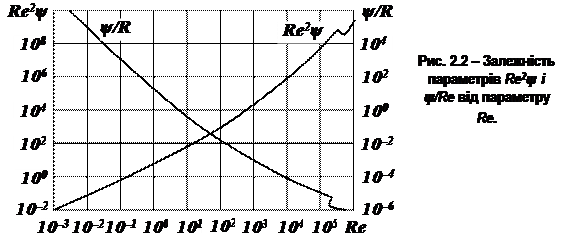Визначення кінцевої швидкості полягає в тому, що при відомих параметрах частинки і середовища розраховується параметр Re²ψ:

Re²ψ = πd³(δ –Δ)gΔ / (6μ²).(2.18)

Потім за діаграмою (рис. 2.2) знаходять значення Re, після чого з використанням формули (2.3) визначають кінцеву швидкість:

V₀ = Reμ / dΔ . (2.19)

За методом Т.Г. Фоменка кінцеві швидкості падіння частинок у середовищі визначають з використанням параметра Архімеда:

Ar = d³(δ - Δ)gΔ / μ². (2.20)

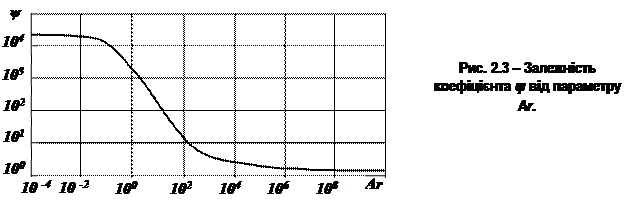
Потім за діаграмою ψ = f(Ar) (рис. 2.3) або за формулою (2.21) знаходять значення коефіцієнта опору ψ і розраховують кінцеву швидкість падіння частинки (2.22):

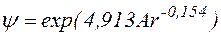; (2.21)

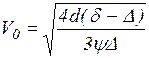, м/с. (2.22)

При груповому русі мінеральних частинок різної густини і крупності завжди існує деяка кількість частинок, що мають однакові швидкості руху в середовищі. Частинки, що при різній густині і крупності мають однакову кінцеву швидкість падіння в одному і тому ж середовищі, називаються рівнопадаючими, а відношення їхніх діаметрів – коефіцієнтом рівнопадання е :

e = d₁ / d₂ =Re₁ / Re₂ (2.23)

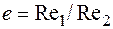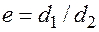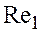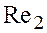де індекс «1» відноситься до частинок меншої густини, індекс «2» – до частинок більшої густини. Використання співвідношення рівнозначно співвідношенню , тому що числа Рейнольдса і (2.3) відрізняються лише розмірами частинок.

З умови рівності кінцевих швидкостей руху частинок коефіцієнт рівнопадання може бути обчислений з використанням густини частинок і середовища:

e = [(δ₂ - Δ) / (δ₁ - Δ)] ⁿ . (2.24)

де n – показник степені, що залежить від режиму руху частинок; при русі в турбулентній області n = 1, у перехідній n = 2/3, у ламінарній n = 0,5.

За методом П.В. Лященка коефіцієнт рівнопадання визначають з використанням параметра ψ/Re . Для частинки меншої густини параметр ψ/Re визначають за формулою:

ψ₁/Re₁ = πg(δ₁ - Δ)μ / (6V₀³Δ²) . (2.25)

Потім по діаграмі Re = f(ψ/Re) (рис. 2.2) знаходять число Рейнольдса для частинки меншої густини – Re₁, з використанням якого визначають параметр ψ/Re для частинки більшої густини:

ψ₂/Re₂ = ψ₁ (δ₂ - Δ) / [Re₁ (δ₁ - Δ)] , (2.26)

знаходять по діаграмі число Рейнольдса Re₂ і визначають коефіцієнт рівнопадання по співвідношенню між числами Рейнольдса за формулою (2.23).

За методом Т.Г.Форменка для частинки меншої густини розраховують відношення:

ψ₁³/Ar₁ = 64 μ²(δ₁ - Δ)²g² / (27V₀⁶Δ⁴) , (2.27)

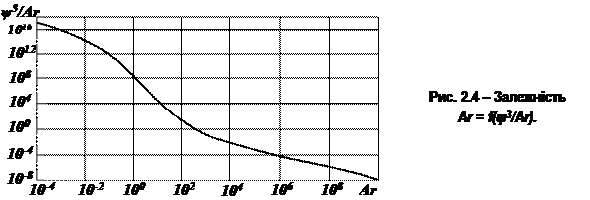
за цим відношенням по діаграмі (рис. 2.4) знаходять значення Ar₁.

Для частинки більшої густини параметр ψ₂³/Ar₂ визначають з використанням раніше обчисленого Ar₁:

ψ₂ ³/Ar₂ = ψ₁ ³(δ₂ - Δ)² / [Ar₁(δ₁ - Δ)²] (2.28)

і по діаграмі Ar = f(ψ³/Ar) знаходять параметр Ar₂ . Для визначення діаметрів рівнопадаючих частинок параметри Ar₁і Ar₂ підставляють у формулу:

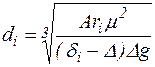. (2.29)

Коефіцієнт рівнопадання визначається за формулою (2.23) як співвідношення діаметрів рівнопадаючих частинок.